Sec of negative angle

A mathematical relation of secant of negative angle with secant of positive angle is called sec of negative angle identity.

Proof

Geometrically, the mathematical relation between secant of negative angle and secant of positive angle can be derived mathematically in trigonometry.

Construction of triangle with positive angle

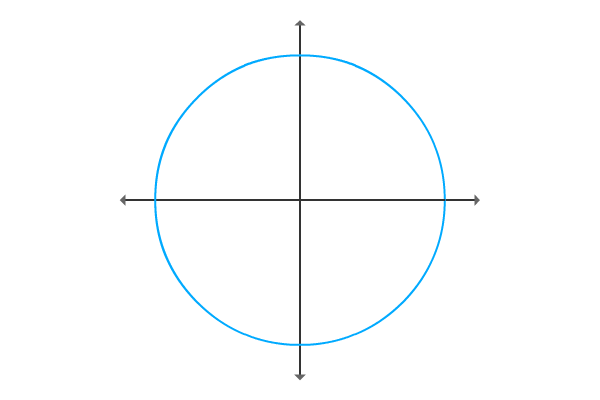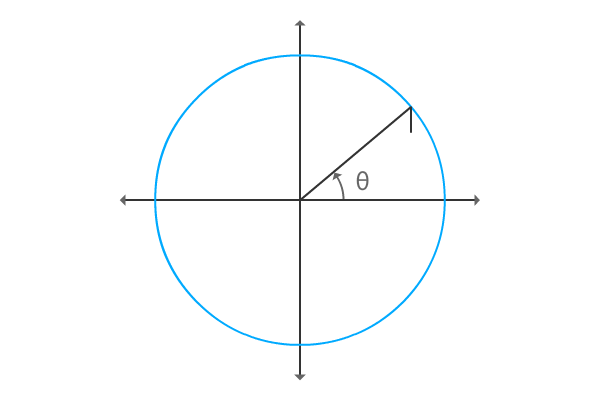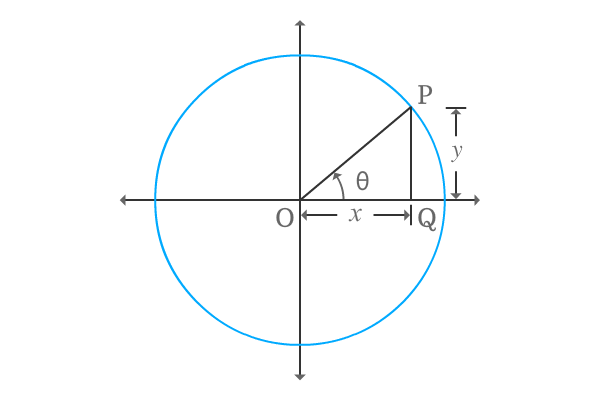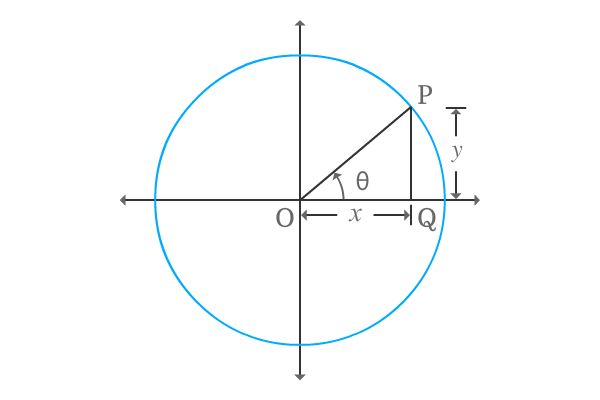
A right angled triangle, called $\Delta POQ$ is constructed with a positive angle theta and secant of angle can be expressed in mathematical form in terms of ratio of lengths of the respective sides.

$\sec{\theta} \,=\, \dfrac{OP}{OQ}$

The right angle triangle $\Delta POQ$ is actually constructed in first quadrant. So, the lengths of adjacent side and opposite side are positive, and assumed to represent them as $x$ and $y$ respectively.

$\implies$ $\sec{\theta} \,=\, \dfrac{\sqrt{x^2+y^2}}{x}$

Construction of triangle with negative angle

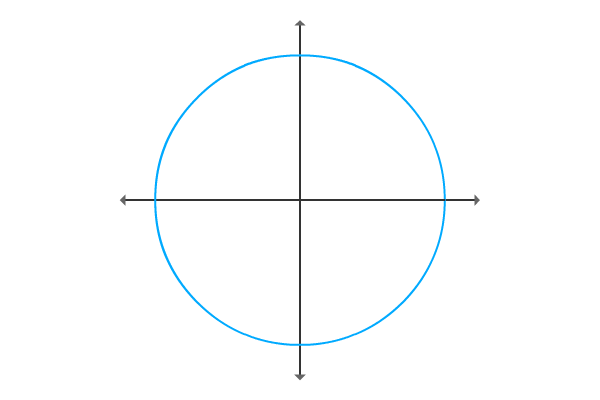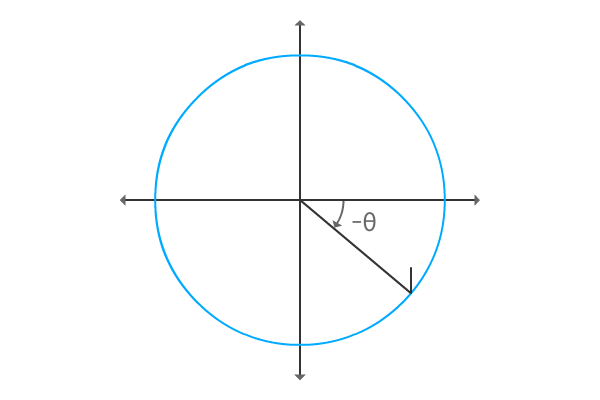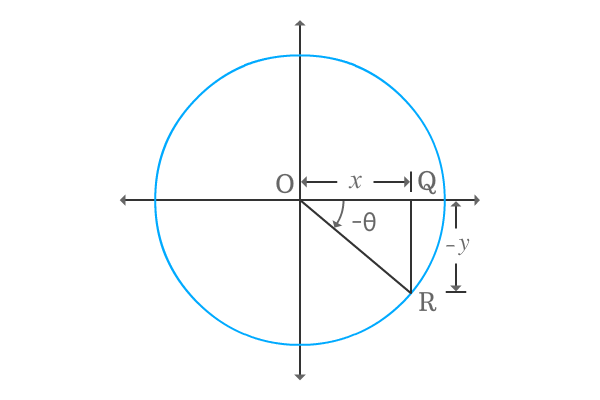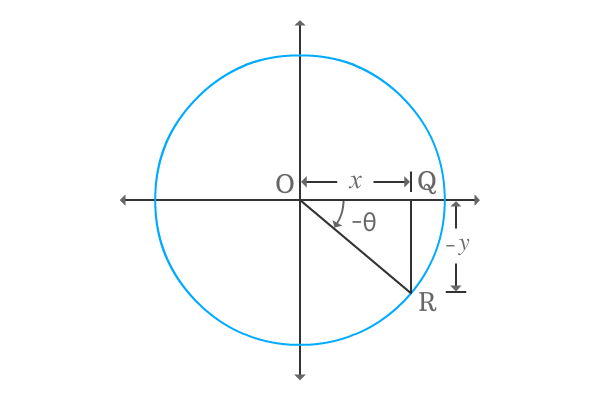
In the same way, construct same right angled triangle but with negative angle. Therefore, the angle of the triangle will be $–\theta$ geometrically.

Now, write trigonometric ratio secant of angle in terms of ratio of lengths of adjacent side and hypotenuse.

$\sec{(-\theta)} \,=\, \dfrac{OR}{OQ}$

In fact, the length of opposite side is $–y$ but the length of adjacent side is same due to construction of triangle with negative angle.

$\implies$ $\sec{(-\theta)} \,=\, \dfrac{\sqrt{x^2+y^2}}{x}$

Comparing Cosine functions

In order to obtain relation between them, compare both equations of secant of positive angle and secant of negative angle.

$\sec{\theta} \,=\, \dfrac{\sqrt{x^2+y^2}}{x}$

$\sec{(-\theta)} \,=\, \dfrac{\sqrt{x^2+y^2}}{x}$

The two equations clearly discloses that secant of negative angle is always equal to secant of angle.

$\,\,\, \therefore \,\,\,\,\,\,$ $\sec{(-\theta)} \,=\, \sec{\theta}$

This trigonometric identity is called secant of negative angle identity and used as a formula sometimes in trigonometric mathematics.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.