Cot of negative angle

A mathematical relation of cotangent of negative angle with cotangent of positive angle is called cot of negative angle identity.

Proof

Actually, the mathematical relation between cotangent of negative angle and cot of positive angle can be derived in mathematical form by geometrical approach in trigonometry.

Construction of triangle with positive angle

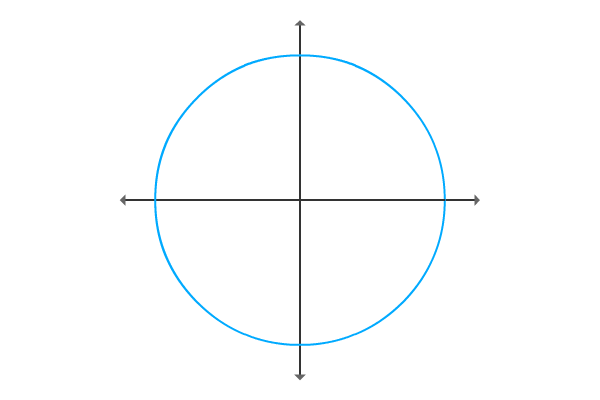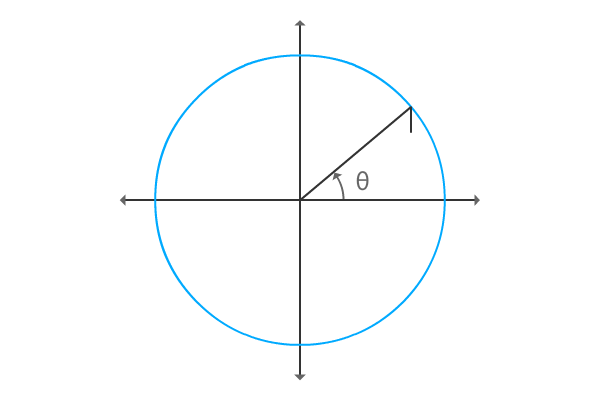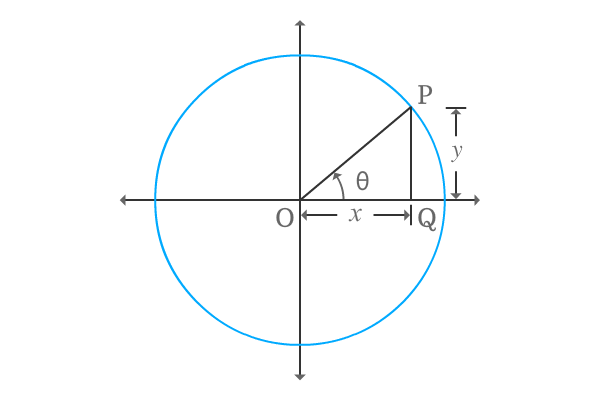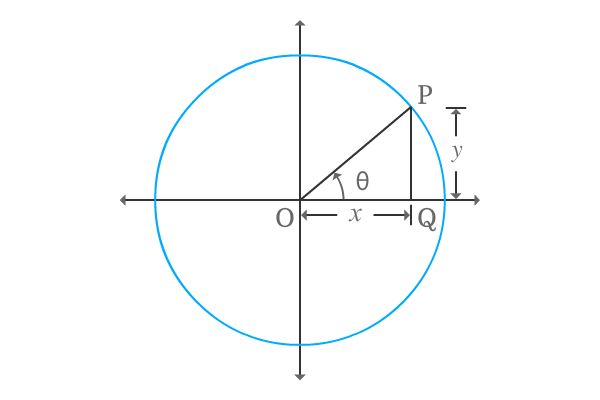
$\Delta POQ$ is a right angled triangle and it is constructed geometrically by taking theta as its angle. Now, write the cot of positive angle in terms of ratio of lengths of the corresponding sides.

$\cot{\theta} \,=\, \dfrac{OQ}{PQ}$

The triangle is actually constructed in first quadrant. So, the lengths of them are positive. Take the lengths of adjacent and opposite sides as $x$ and $y$ respectively.

$\implies$ $\cot{\theta} \,=\, \dfrac{x}{y}$

Construction of triangle with negative angle

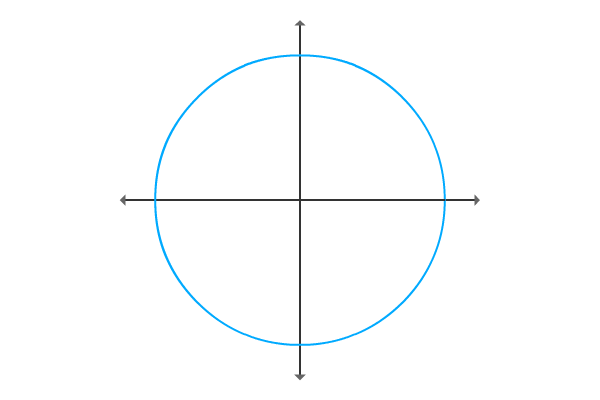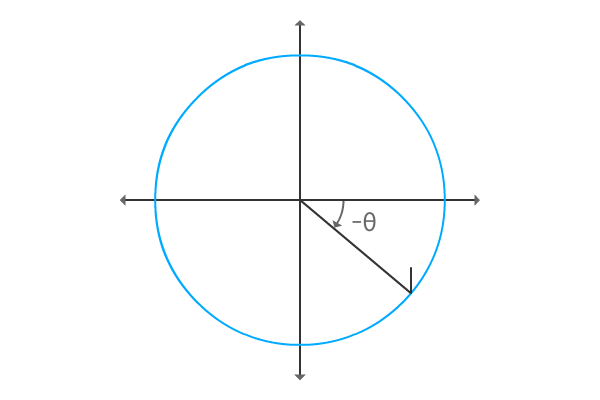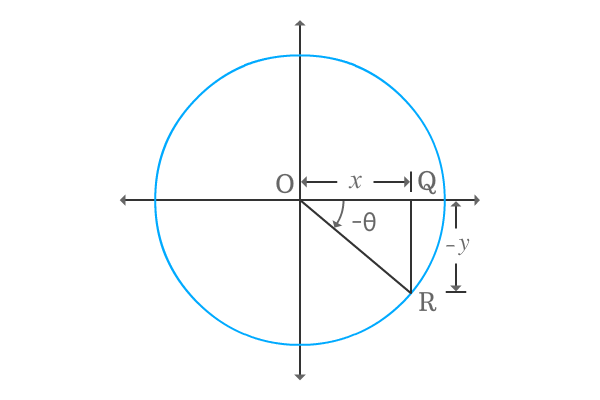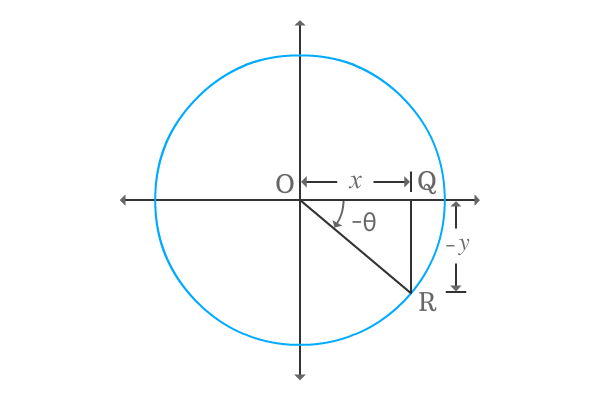
Construct same right angled triangle with negative angle. So, its angle will be negative and the angle of $\Delta ROQ$ is negative theta, represented by $–\theta$ mathematically.

According to this, express the cot of negative angle in terms of ratio of lengths of corresponding sides.

$\cot{(-\theta)} \,=\, \dfrac{OQ}{QR}$

The length of opposite side is $–y$ because of constructing triangle with negative angle.

$\implies$ $\cot{(-\theta)} \,=\, \dfrac{x}{-y}$

$\implies$ $\cot{(-\theta)} \,=\, -\dfrac{x}{y}$

Comparing Cosine functions

Now, compare equation of cotangent of positive angle with cot of negative angle.

$\cot{\theta} \,=\, \dfrac{x}{y}$

$\cot{(-\theta)} \,=\, -\dfrac{x}{y}$

The two equations express that cot of negative angle is always equal to negative of cot of angle.

$\,\,\, \therefore \,\,\,\,\,\,$ $\cot{(-\theta)} \,=\, -\cot{\theta}$

It is called cot of negative angle identity and generally used as a formula in trigonometry mathematics.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.