Two times logarithm of $a$ to the base $x$ plus logarithm of $a$ to the base $a$ times $x$ plus three times logarithm of $a$ to the base $a$ square times $x$ equals to zero is the given logarithmic equation in this log problem. In this logarithmic equation, the literal $a$ represents a constant and $x$ denotes a variable, and the value of $x$ should be evaluated by solving the logarithmic equation.
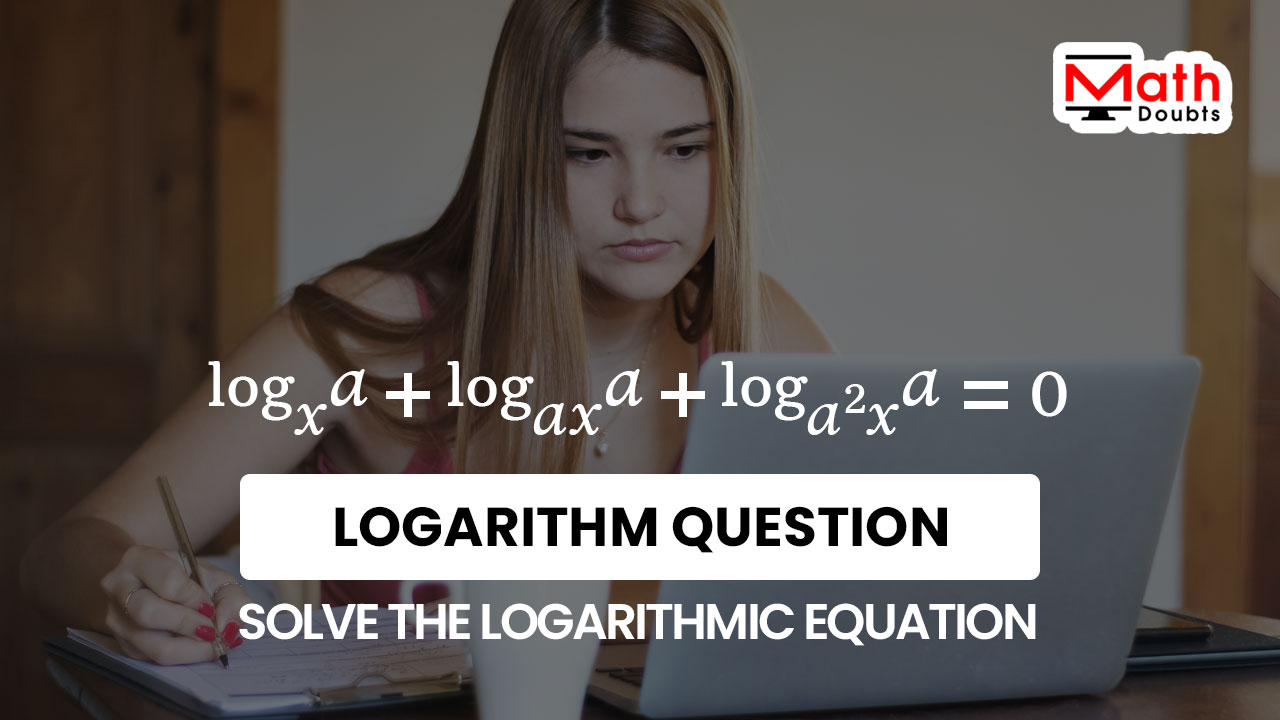
So, let’s learn how to solve the $2$ times log of $a$ to base $x$ plus log of $a$ to base $ax$ plus $3$ times log of $a$ to base $a^2x$ is equal to $0$.
Look at each term in the logarithmic equation. All logarithmic functions have different bases, and they are $x$, $ax$ and $a^2x$ respectively, and it stops us in adding the logarithmic terms mathematically.
$\implies$ $2 \times \log_{\large x}{a}$ $+$ $\log_{\large ax}{a}$ $+$ $3 \times \log_{\large a^2x}{a}$ $\,=\,$ $0$
However, it is possible to add if all logarithmic functions in the equation have the same base, and it is possible by changing the base with quantity as per the switch rule of logarithms.
$\implies$ $2 \times \dfrac{1}{\log_{\large a}{x}}$ $+$ $\dfrac{1}{\log_{\large a}{ax}}$ $+$ $3 \times \dfrac{1}{\log_{\large a}{a^2x}}$ $\,=\,$ $0$
Now, multiply the factors in each term by the multiplication rule of the fractions and it expresses the logarithmic equation appropriately.
$\implies$ $\dfrac{2 \times 1}{\log_{\large a}{x}}$ $+$ $\dfrac{1}{\log_{\large a}{ax}}$ $+$ $\dfrac{3 \times 1}{\log_{\large a}{a^2x}}$ $\,=\,$ $0$
$\implies$ $\dfrac{2}{\log_{\large a}{x}}$ $+$ $\dfrac{1}{\log_{\large a}{ax}}$ $+$ $\dfrac{3}{\log_{\large a}{a^2x}}$ $\,=\,$ $0$
In the second and third terms, the quantities inside the logarithmic function are in product form.
$\implies$ $\dfrac{2}{\log_{\large a}{x}}$ $+$ $\dfrac{1}{\log_{\large a}{(a \times x)}}$ $+$ $\dfrac{3}{\log_{\large a}{(a^2 \times x)}}$ $\,=\,$ $0$
The logarithm of a product can be calculated by the summation of their logarithms as per the product rule of the logarithms.
$\implies$ $\dfrac{2}{\log_{\large a}{x}}$ $+$ $\dfrac{1}{\log_{\large a}{a}+\log_{\large a}{x}}$ $+$ $\dfrac{3}{\log_{\large a}{a^2}+\log_{\large a}{x}}$ $\,=\,$ $0$
In the third term, the constant $a$ is in square form. The logarithm of $a$ square can be written as two times logarithm of $a$ as per the power rule of logarithms.
$\implies$ $\dfrac{2}{\log_{\large a}{x}}$ $+$ $\dfrac{1}{\log_{\large a}{a}+\log_{\large a}{x}}$ $+$ $\dfrac{3}{2 \times \log_{\large a}{a}+\log_{\large a}{x}}$ $\,=\,$ $0$
Use the logarithm of base rule and the logarithm of $a$ to the base $a$ is equal to one as per this log identity.
$\implies$ $\dfrac{2}{\log_{\large a}{x}}$ $+$ $\dfrac{1}{1+\log_{\large a}{x}}$ $+$ $\dfrac{3}{2 \times 1+\log_{\large a}{x}}$ $\,=\,$ $0$
$\implies$ $\dfrac{2}{\log_{\large a}{x}}$ $+$ $\dfrac{1}{1+\log_{\large a}{x}}$ $+$ $\dfrac{3}{2+\log_{\large a}{x}}$ $\,=\,$ $0$
The logarithmic equation is expressed in terms of logarithm of $x$ to the base $a$. In order to, avoid the confusion while solving this equation, denote the logarithm of $x$ to the base $a$ by a variable $y$.
$\implies$ $\dfrac{2}{y}$ $+$ $\dfrac{1}{1+y}$ $+$ $\dfrac{3}{2+y}$ $\,=\,$ $0$
Now, the logarithmic equation is converted as an algebraic equation in terms of $y$. Let us simplify the logarithmic equation firstly and it makes the equation easier for solving. $y$ is an expression in the denominator of the first term. So, multiply both sides of the expression by $y$.
$\implies$ $y \times \bigg(\dfrac{2}{y}$ $+$ $\dfrac{1}{1+y}$ $+$ $\dfrac{3}{2+y}\bigg)$ $\,=\,$ $y \times 0$
On the left hand side of the equation, $y$ is a coefficient of three terms and it can be distributed to all the terms by the distributive property of multiplication over the addition. Multiply the variable $y$ by zero on the right hand side of the equation and their product is equal to zero.
$\implies$ $y \times \dfrac{2}{y}$ $+$ $y \times \dfrac{1}{1+y}$ $+$ $y \times \dfrac{3}{2+y}$ $\,=\,$ $0$
Now, multiply the factors in all three terms by the multiplication rule of the fractions.
$\implies$ $\dfrac{y \times 2}{y}$ $+$ $\dfrac{y \times 1}{1+y}$ $+$ $\dfrac{y \times 3}{2+y}$ $\,=\,$ $0$
$\implies$ $\dfrac{\cancel{y} \times 2}{\cancel{y}}$ $+$ $\dfrac{y \times 1}{1+y}$ $+$ $\dfrac{y \times 3}{2+y}$ $\,=\,$ $0$
$\implies$ $2$ $+$ $\dfrac{y \times 1}{1+y}$ $+$ $\dfrac{3 \times y}{2+y}$ $\,=\,$ $0$
$\implies$ $2$ $+$ $\dfrac{y}{1+y}$ $+$ $\dfrac{3y}{2+y}$ $\,=\,$ $0$
$1+y$ is an expression in the denominator of the second term. So, multiply the expressions on both sides of the equation by $1+y$.
$\implies$ $(1+y) \times \bigg(2$ $+$ $\dfrac{y}{1+y}$ $+$ $\dfrac{3y}{2+y}\bigg)$ $\,=\,$ $(1+y) \times 0$
Likewise, distributive the coefficient $1+y$ to all the terms on left hand side and multiply the $1+y$ by zero on the right hand side of the equation. After that, calculate the product of the factors in the terms of both sides of the equation.
$\implies$ $(1+y) \times 2$ $+$ $(1+y) \times \dfrac{y}{1+y}$ $+$ $(1+y) \times \dfrac{3y}{2+y}$ $\,=\,$ $0$
$\implies$ $(1+y) \times 2$ $+$ $\dfrac{(1+y) \times y}{1+y}$ $+$ $\dfrac{(1+y) \times 3y}{2+y}$ $\,=\,$ $0$
$\implies$ $2 \times (1+y)$ $+$ $\dfrac{y \times (1+y)}{1+y}$ $+$ $\dfrac{3y \times (1+y)}{2+y}$ $\,=\,$ $0$
$\implies$ $2(1+y)$ $+$ $\dfrac{y \times \cancel{(1+y)}}{\cancel{1+y}}$ $+$ $\dfrac{3y \times (1+y)}{2+y}$ $\,=\,$ $0$
$\implies$ $2(1+y)$ $+$ $y$ $+$ $\dfrac{3y(1+y)}{2+y}$ $\,=\,$ $0$
$2+y$ is an expression in the denominator of the third term. Now, multiply the expressions on both sides of the equation by $2+y$. Similarly, repeat the same procedure to eliminate the rational form completely from all the terms.
$\implies$ $(2+y)$ $\times$ $\bigg(2(1+y)$ $+$ $y$ $+$ $\dfrac{3y(1+y)}{2+y}\bigg)$ $\,=\,$ $(2+y) \times 0$
$\implies$ $(2+y) \times 2(1+y)$ $+$ $(2+y) \times y$ $+$ $(2+y) \times \dfrac{3y(1+y)}{2+y}$ $\,=\,$ $0$
$\implies$ $2(1+y) \times (2+y)$ $+$ $y \times (2+y)$ $+$ $\dfrac{(2+y) \times 3y(1+y)}{2+y}$ $\,=\,$ $0$
$\implies$ $2(1+y)(2+y)$ $+$ $y(2+y)$ $+$ $\dfrac{\cancel{(2+y)} \times 3y(1+y)}{\cancel{2+y}}$ $\,=\,$ $0$
$\implies$ $2(1+y)(2+y)$ $+$ $y(2+y)$ $+$ $3y(1+y)$ $\,=\,$ $0$
It is time to find the product of the factors in each term on the left hand side of the equation.
$\implies$ $2(1 \times 2$ $+$ $1 \times y$ $+$ $y \times 2$ $+$ $y \times y)$ $+$ $y \times 2$ $+$ $y \times y$ $+$ $3y \times 1$ $+$ $3y \times y$ $\,=\,$ $0$
Now, let’s focus on simplifying the algebraic expression on the left hand side of the equation.
$\implies$ $2(2$ $+$ $y$ $+$ $2y$ $+$ $y^2)$ $+$ $2y$ $+$ $y^2$ $+$ $3y$ $+$ $3y^2$ $\,=\,$ $0$
$\implies$ $2(2$ $+$ $3y$ $+$ $y^2)$ $+$ $2y$ $+$ $y^2$ $+$ $3y$ $+$ $3y^2$ $\,=\,$ $0$
$\implies$ $2 \times 2$ $+$ $2 \times 3y$ $+$ $2 \times y^2$ $+$ $2y$ $+$ $y^2$ $+$ $3y$ $+$ $3y^2$ $\,=\,$ $0$
$\implies$ $4$ $+$ $6y$ $+$ $2y^2$ $+$ $2y$ $+$ $y^2$ $+$ $3y$ $+$ $3y^2$ $\,=\,$ $0$
$\implies$ $2y^2$ $+$ $y^2$ $+$ $3y^2$ $+$ $6y$ $+$ $2y$ $+$ $3y$ $+$ $4$ $\,=\,$ $0$
$\,\,\,\therefore\,\,\,\,\,\,$ $6y^2$ $+$ $11y$ $+$ $4$ $\,=\,$ $0$
The six times $y$ square plus eleven times $y$ plus four equals to zero is a quadratic equation and it can be solved in any method. Now, let’s solve the quadratic equation by factoring method.
The coefficient of $y$ square is $6$ and the constant term is $4$, and the product of them is $24$.
$\implies$ $6 \times 4$ $\,=\,$ $24$
Now, consider the factors of $24$ to check whether the sum or difference of its factors is equal to coefficient of $y$, which means $11$. The factors $3$ and $8$ are factors of twenty four and their sum is equal to the coefficient of $y$.
$\,\,\,\therefore\,\,\,\,\,\,$ $3 \times 8$ $\,=\,$ $24$ and $3+8$ $\,=\,$ $11$
Therefore, the middle term of the quadratic expression can be split as follows.
$\implies$ $6y^2$ $+$ $3y$ $+$ $8y$ $+$ $4$ $\,=\,$ $0$
Now, let us focus on taking out the common factors from the terms for factorizing the quadratic expression in the equation.
$\implies$ $3y \times 2y$ $+$ $3y \times 1$ $+$ $4 \times 2y$ $+$ $4 \times 1$ $\,=\,$ $0$
$\implies$ $3y \times (2y+1)$ $+$ $4 \times (2y+1)$ $\,=\,$ $0$
$\implies$ $(2y+1)(3y+4)$ $\,=\,$ $0$
$\implies$ $2y+1 \,=\, 0$ or $3y+4 \,=\, 0$
$\implies$ $2y \,=\, -1$ or $3y \,=\, -4$
$\,\,\,\therefore\,\,\,\,\,\,$ $y \,=\, -\dfrac{1}{2}$ or $y \,=\, -\dfrac{4}{3}$
Therefore, the solution set of the quadratic equation $6$ times $y$ square plus $11$ times $y$ plus $4$ equals to zero is written as $\bigg\{-\dfrac{4}{3}, -\dfrac{1}{2}\bigg\}$.
The given logarithmic equation in this problem is defined in terms of $x$ but we obtained the values of $y$. So, replace the value of variable $y$ in terms of $x$ to find the solutions. We have assumed that the variable $y$ is considered to denote the logarithm of $x$ to the base $a$. So, replace the variable $y$ by substituting $\log$ of $x$ to the base $a$.
$\implies$ $\log_{\large a}{x} \,=\, -\dfrac{1}{2}$ or $\log_{\large a}{x} \,=\, -\dfrac{4}{3}$
The logarithmic operation can be released from the equations by using the relationship between the logarithms and exponentiation.
$\implies$ $x \,=\, a^{- \Large \frac{1}{2}}$ or $x \,=\, a^{- \Large \frac{4}{3}}$
Now, use the negative exponent rule to express the quantities with negative exponents in reciprocal form.
$\implies$ $x \,=\, \dfrac{1}{a^{\Large \frac{1}{2}}}$ or $x \,=\, \dfrac{1}{a^{\Large \frac{4}{3}}}$
Finally, let us write the exponents in irrational form in root form for writing the solutions of the given logarithmic equation in simple form.
$\,\,\,\therefore\,\,\,\,\,\,$ $x \,=\, \dfrac{1}{\sqrt{a}}$ or $x \,=\, \dfrac{1}{\sqrt[\Large 3]{a^4}}$
Therefore, the solution set of the logarithmic equation $2$ times log of $a$ to base $x$ plus log of $a$ to base $ax$ plus $3$ times log of $a$ to base $a$ square $x$ equals to $0$ is written as $\bigg\{\dfrac{1}{\sqrt{a}}, \dfrac{1}{\sqrt[\Large 3]{a^4}}\bigg\}$ in mathematics.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved