Negative angle

Definition

The amount of rotation of ray from its initial position to final position in clockwise direction is called negative angle.

Clockwise direction is considered as negative direction in the case of angle. There is a universally accepted reason to consider clockwise direction as negative direction. Every book is closed in clockwise direction and we think it is a finishing of reading or writing. So, the clockwise direction is considered as negative direction in the case of angle.

Negative angles are written in mathematics by displaying minus sign $(-)$ before the angle.

Example

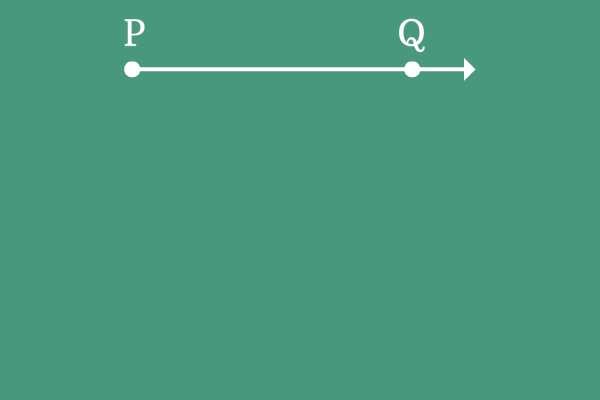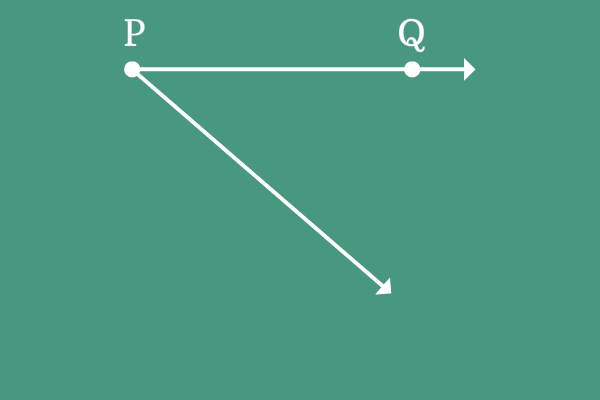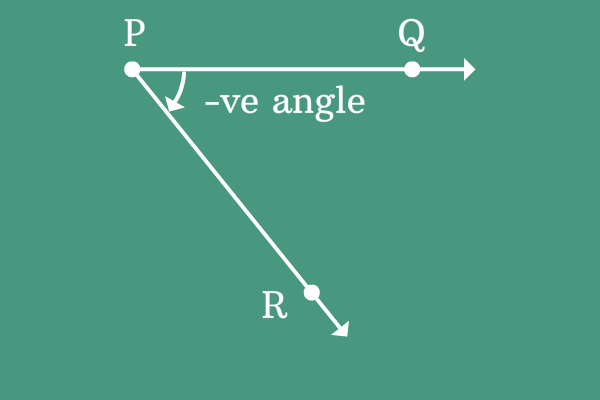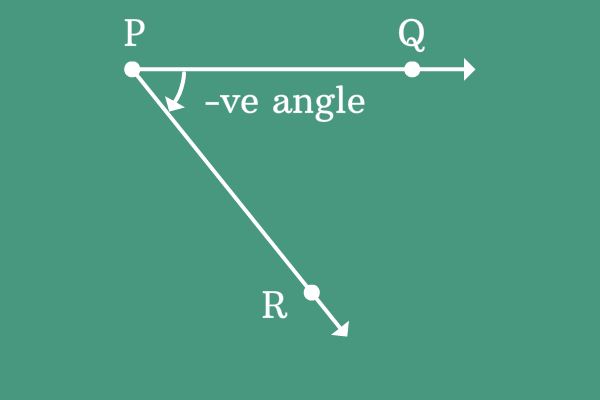
$\overrightarrow{PQ}$ is a ray and it is initially at a position on the plane.

The ray $\overrightarrow{PQ}$ is rotated in clockwise direction and reached its final position where the same ray is known as ray $\overrightarrow{PR}$.

The direction of angle made by the ray is clockwise and it is considered as negative direction.

Therefore, the angle made by the ray $\overrightarrow{PQ}$ to become $\overrightarrow{PR}$ is known as negative angle.

For example, if an angle is $40^°$ and it is made in clockwise direction, it is written as $-40^°$ in mathematics.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.