Linear equations in One variable

An equation that represents a straight line in terms of one variable is called a linear equation in one variable.

Introduction

In some cases, the mathematical equations are formed in terms of a variable. If the exponent of the variable in the equation is one, then the equation represents a straight line geometrically. So, an equation, which is written in terms of a variable is called the linear equation in one variable.

Example

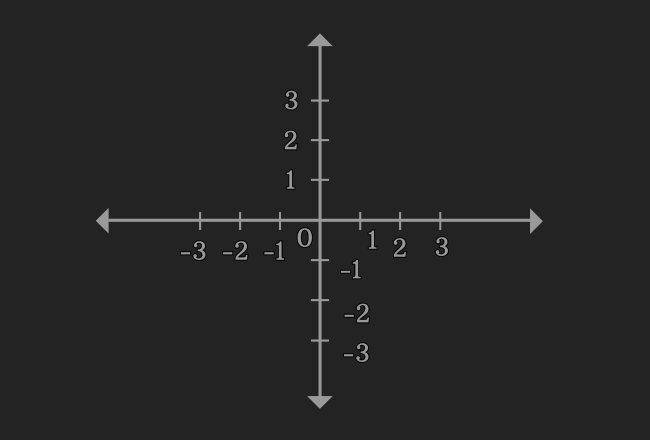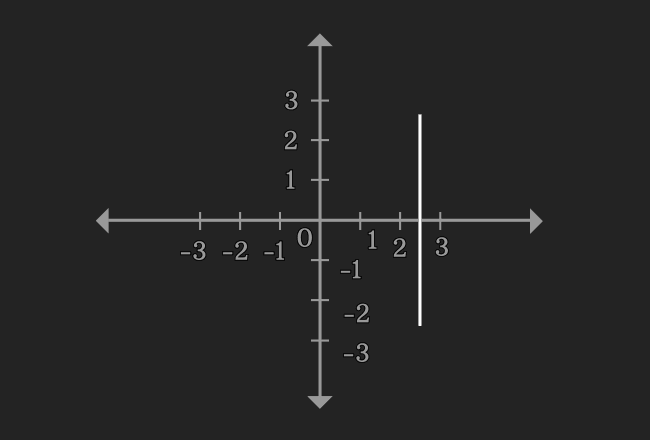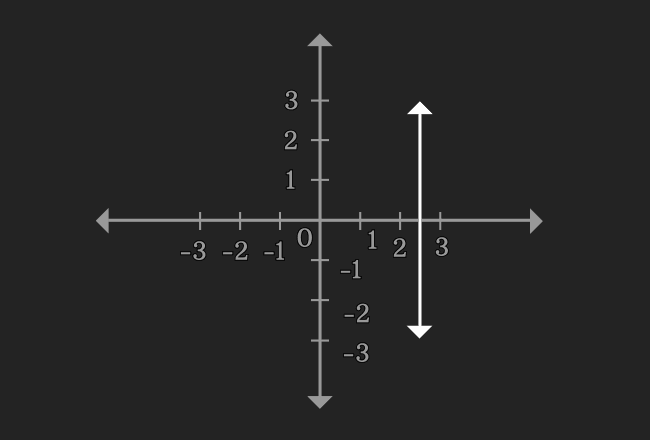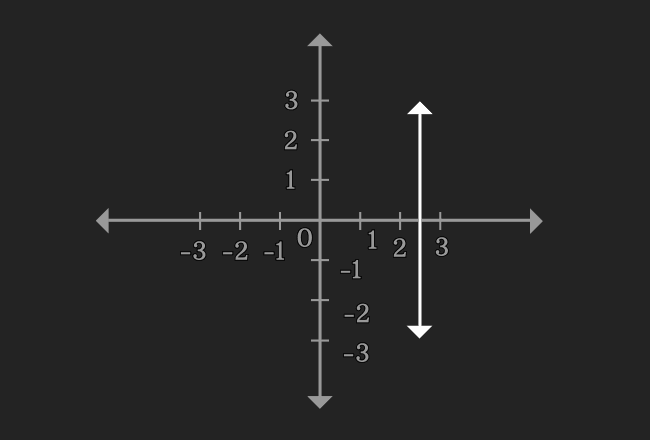
$2x-5 = 0$
It is an equation, which is written in terms of a variable $x$. Now, evaluate $x$.

$\implies$ $2x = 5$

$\implies$ $x = \dfrac{5}{2}$

$\implies$ $\require{cancel} x = \dfrac{\cancel{5}}{\cancel{2}}$

$\implies$ $x = 2.5$

Now, draw a graph for $x = 2.5$ in two dimensional Cartesian coordinate system. You observe that it is a straight line. Therefore, the equation $2x-5 = 0$ is called as a linear equation in one variable.

Examples

Here is some more examples for the linear equations in one variable.

1. $x+9 = 0$
2. $-7p = 3$
3. $3l-\sqrt{8} = 0$
4. $y+1.72 = 0$
5. $4s-1 = 0$

Algebraic form

$a$ and $b$ are two constants but $x$ is a variable. The linear equation in one variable is written in algebraic form mathematically as follows.

$ax+b = 0$

Solving methods

In algebraic mathematics, there are three different methods to solve the linear equations in one variable.

1. Trial and Error
2. Inverse Operations
3. Transposition

Learn each method with understandable solved problems to study how to solve linear equations in one variable.