Indefinite integral calculus

A mathematical science that helps us to calculate the integral of a function without defining its interval is called the indefinite integral calculus.

Introduction

The concept of calculating the indefinite integral of a function can be understood in calculus by constructing a graph geometrically.

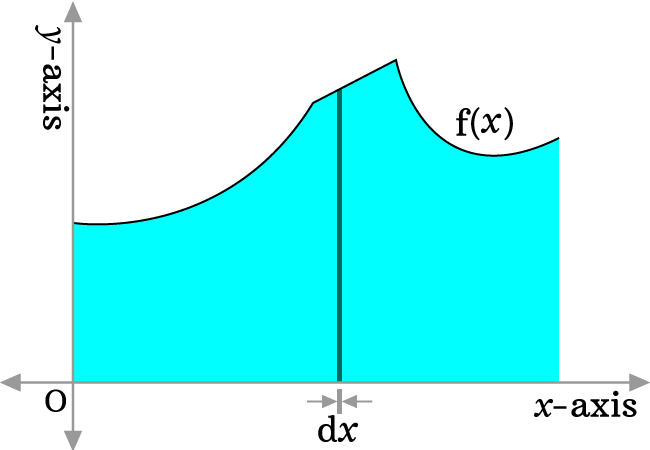
Let $f(x)$ be a mathematical function in terms of $x$. Construct a graph by representing the values of $x$ on the horizontal axis and the values of the function on the vertical axis. The area under the curve is denoted by sea-blue color (or colour).

In order to find the area under the curve, split the whole area into infinitely small equal parts. Now, consider a small part, which is denoted by a differential $dx$.

$\displaystyle \int{f(x)\,}dx$

Integral rules

The list of the indefinite integration formulas with mathematical proofs.

Problems

The list of indefinite integration questions with step by step procedure to learn how to find the indefinite integration of a function by using the integral rules.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.