A point where any two sides of a triangle meet, is called a vertex of a triangle.
Geometrically, a triangle is formed by the intersection of three line segments. Each side of a triangle has two endpoints and the endpoints of all three sides are intersected possibly at three different points in a plane for forming a triangle. The three different intersecting points of them are called vertices of a triangle.
$\Delta PQR$ is a triangle and it is formed by three line segments.
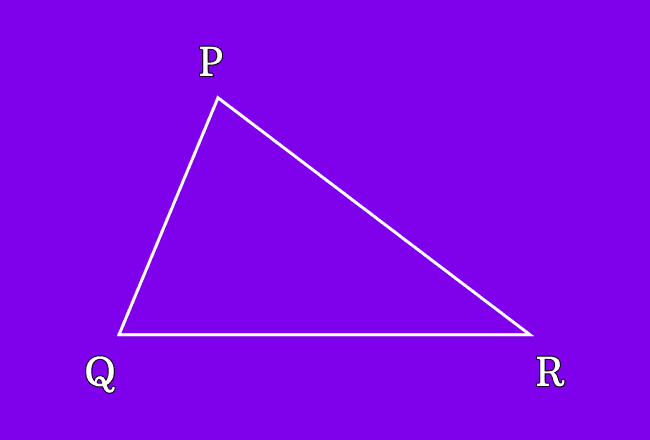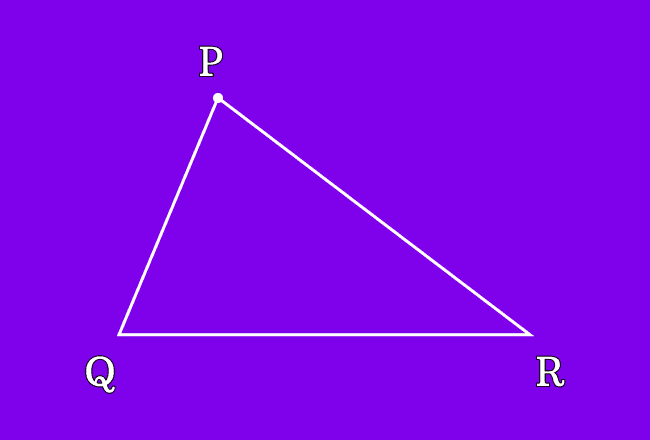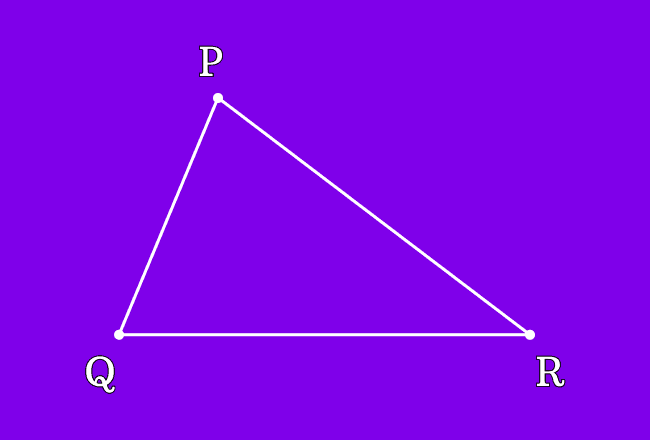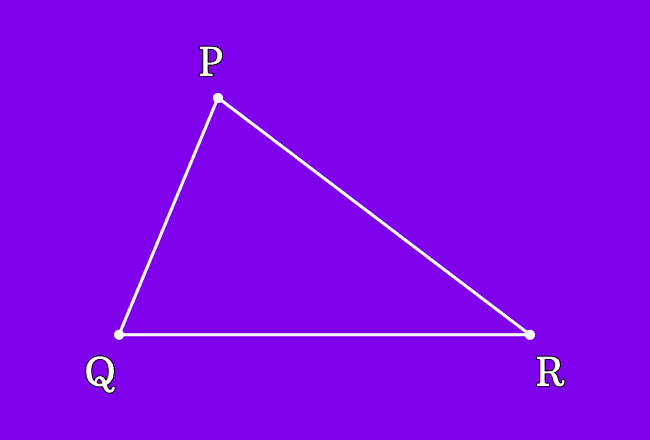
Therefore, the intersecting points $P$, $Q$ and $R$ are called the vertices of the triangle $PQR$.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved