Median

A straight line that joins a vertex and midpoint of its opposite side in a triangle is called a median.

Introduction

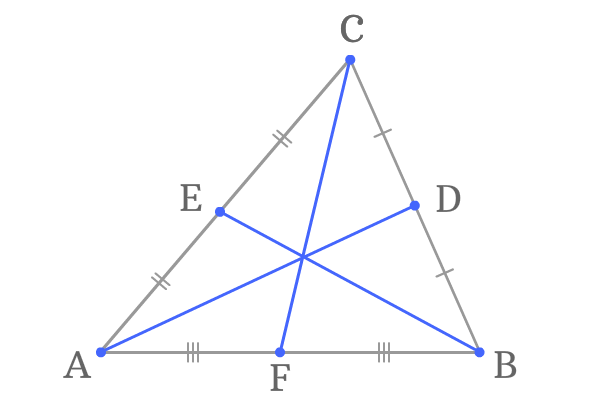
A vertex of a triangle and middle point of opposite side of that vertex are joined by a straight line for a purpose in geometry and the straight line is called a median of the triangle.

Every triangle has three sides and they are actually opposite to three vertices. So, three vertices can be joined with the midpoints of their opposite sides by three line segments. Hence, three medians are formed geometrically in a triangle.

Example

$\Delta ABC$ is a triangle. Its vertices are $A$, $B$ and $C$ and its sides are $\overline{AB}$, $\overline{BC}$ and $\overline{CA}$.

First Median

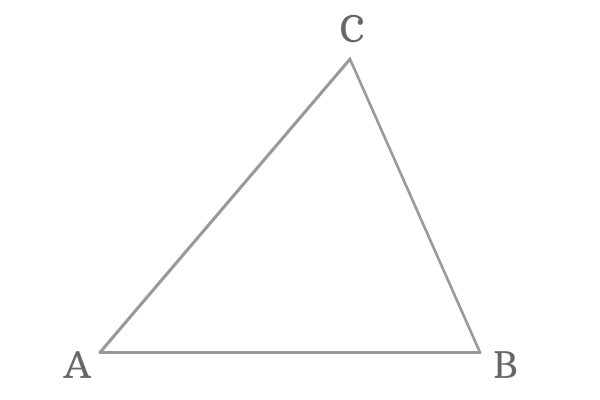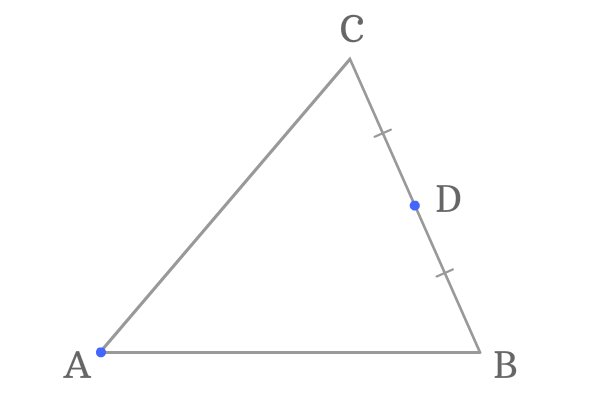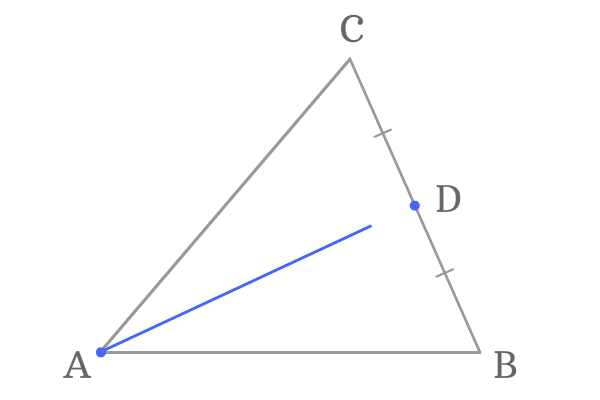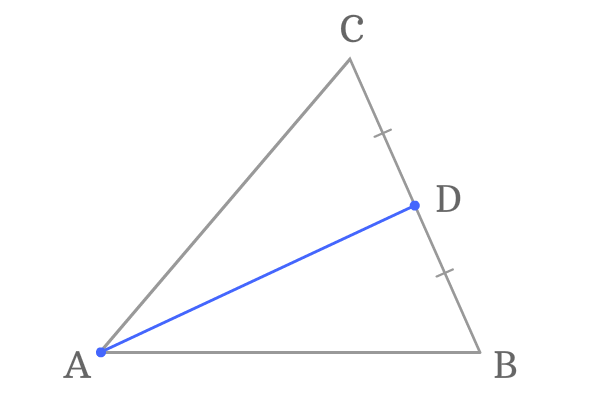
Point $A$ is a vertex and its opposite side is $\overline{BC}$. The point $D$ is a midpoint on the side $\overline{BC}$.

Join the vertex $A$ and the midpoint $D$ by a line. It formed a line segment $\overline{AD}$ and it is known as a median of the triangle.

Second Median

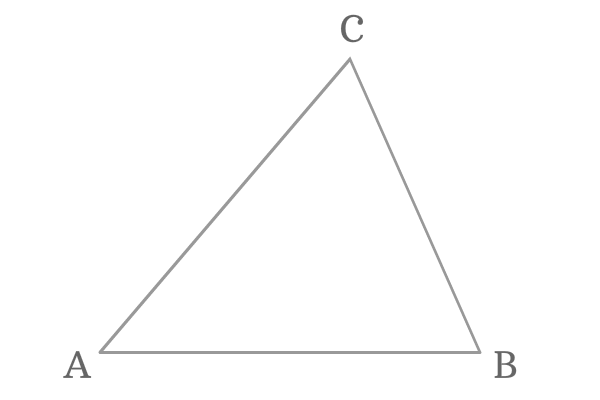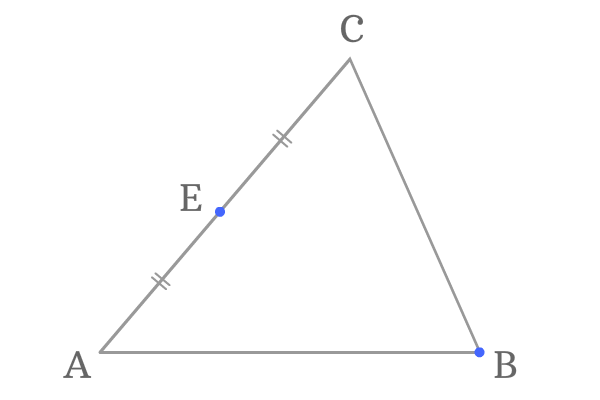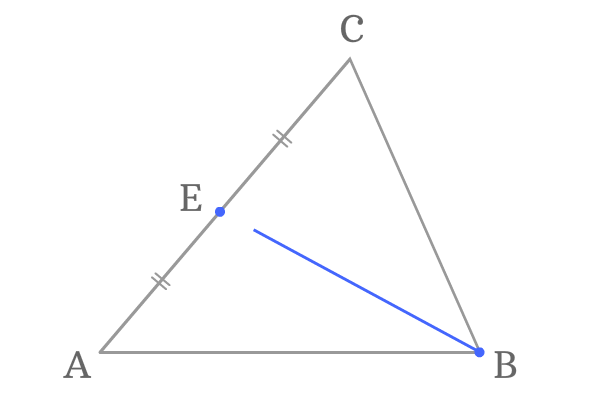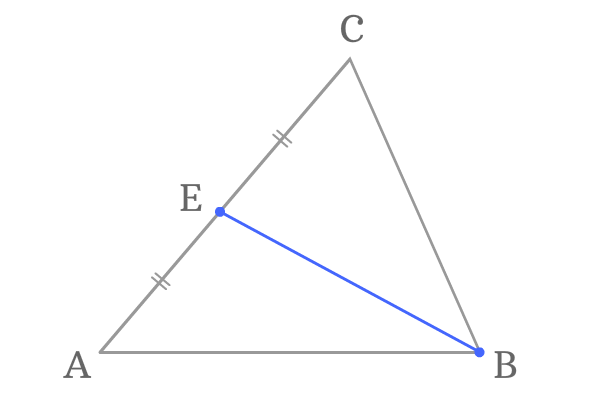
Point $B$ is another vertex of the $\Delta ABC$ and $\overline{AC}$ is its opposite side. The point $E$ is the middle point on the side $\overline{AC}$.

A line segment, represented as $\overline{BE}$ is formed by joining the vertex $B$ and middle point $E$ by a line segment and it is called a median of the triangle.

Third Median

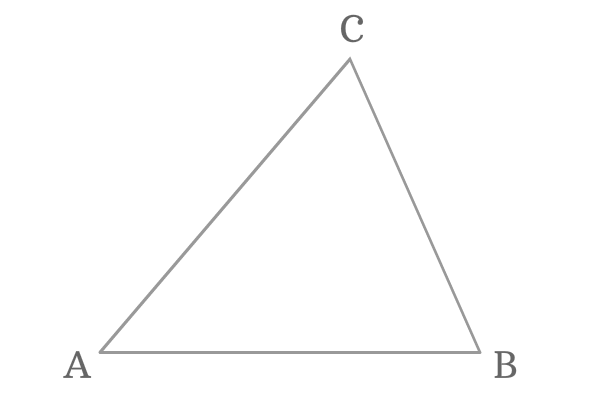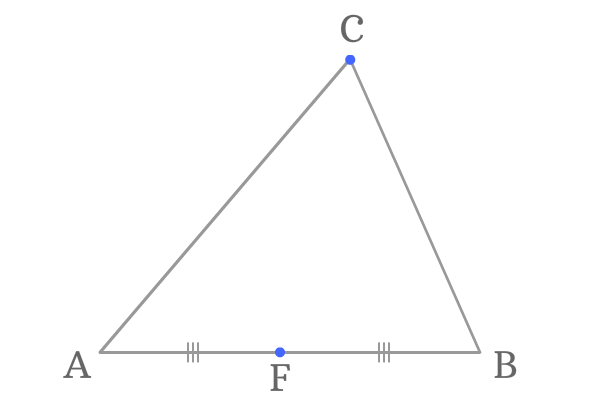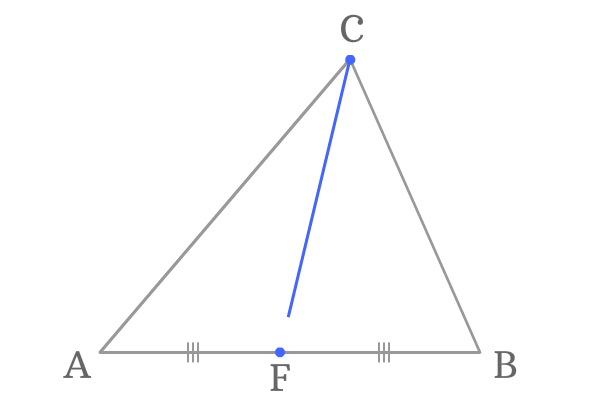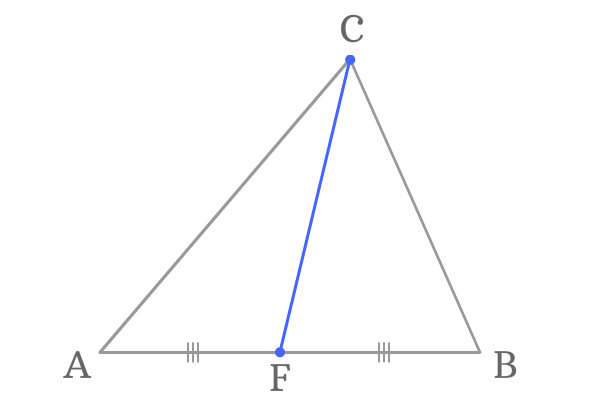
Point $C$ is another vertex of the triangle and its opposite side is $\overline{AB}$. The point $F$ is exact middle point of the side $\overline{AB}$.

Join the vertex $C$ and middle point $F$ by a line. It forms a line segment $\overline{CF}$ and it is known as a median of the triangle.

Thus, three medians are formed geometrically in any type of triangle. In $\Delta ABC$, the line segments $\overline{AD}$, $\overline{BE}$, and $\overline{CF}$ are three medians of the triangle.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.