$d = \sqrt{{(x_{2}-x_{1})}^2+{(y_{2}-y_{1})}^2}$
It is a distance formula and used to find the distance between any two points in a two dimensional Cartesian coordinate system. Now, learn how to derive the distance formula in geometry.
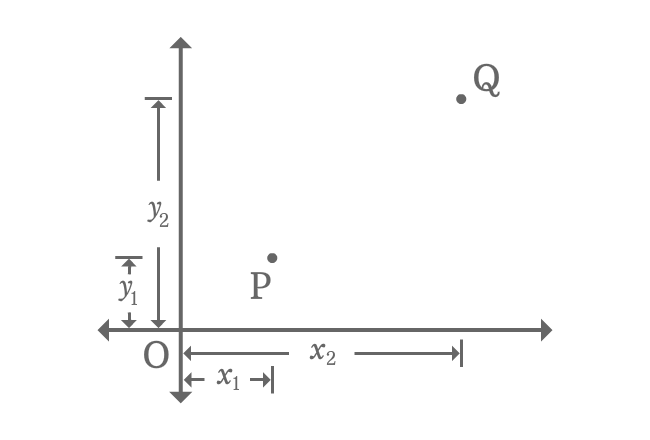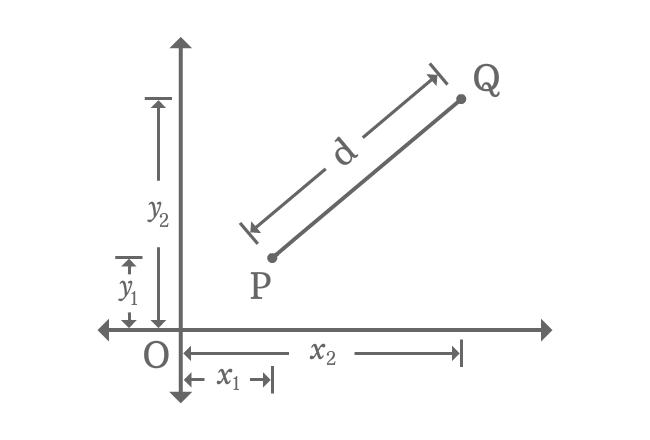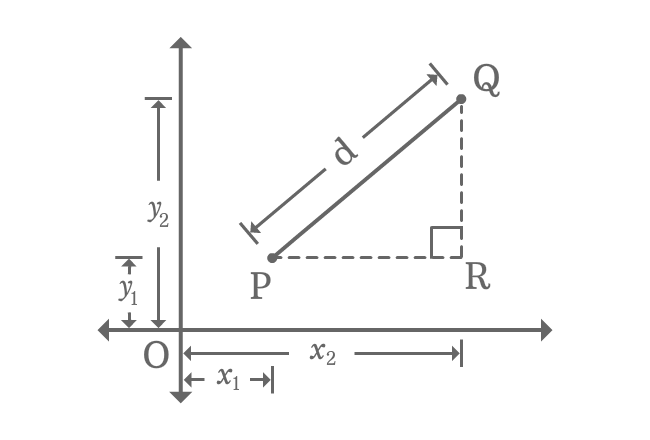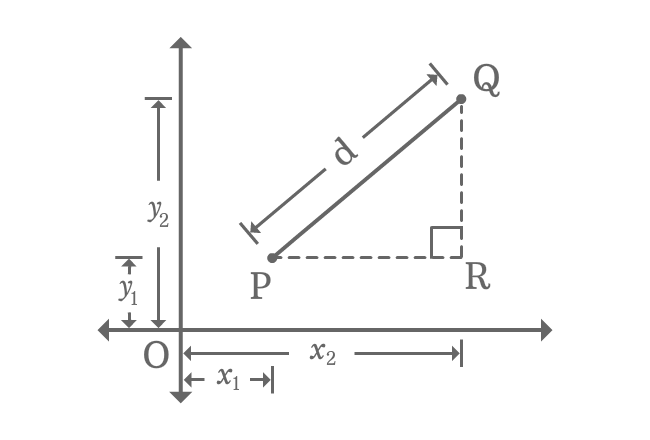
$\overline{PQ}$, $\overline{QR}$ and $\overline{PR}$ are hypotenuse, opposite side (perpendicular) and adjacent side (Base) of right triangle $RPQ$. Now, calculate the length of each side in terms of coordinates of the points.
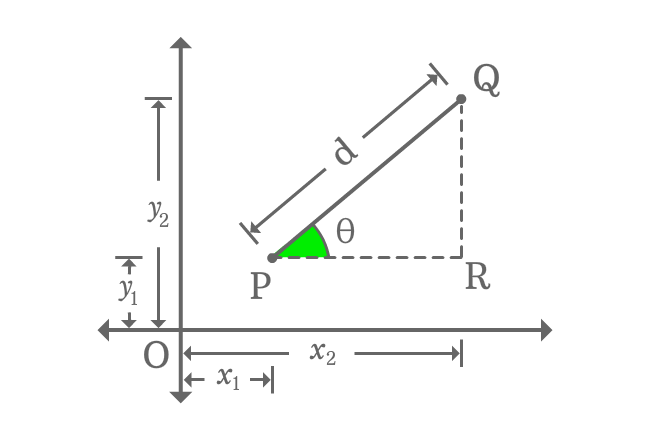
Use this data to find the distance between any two points in a two dimensional Cartesian coordinate system.
The relation between three sides can be written in mathematical form by Pythagorean Theorem.
${PQ}^2 = {PR}^2+{QR}^2$
Substitute lengths of the all three sides.
$\implies d^2 = {(x_2-x_1)}^2+{(y_2-y_1)}^2$
$\implies d = \pm \sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$
The distance is a positive factor physically.
$\,\,\, \therefore \,\,\,\,\,\, d = \sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$
It is called distance formula and used to find distance between any points in a plane. The distance formula reveals that the distance between any two points in a plane is equal to square root of sum of squares of differences of the coordinates.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved