How to find the Cofactors of entries in a 3×3 Matrix in Algebraic form

Let $A$ be a square matrix of order $3$, and their entries are denoted by $e_{11}$, $e_{12}$, $e_{13}$, $e_{21}$, $e_{22}$, $e_{23}$, $e_{31}$, $e_{32}$ and $e_{33}$ in algebraic form.

$A$ $\,=\,$ $\begin{bmatrix} e_{11} & e_{12} & e_{13} \\ e_{21} & e_{22} & e_{23} \\ e_{31} & e_{32} & e_{33} \\ \end{bmatrix}$

Now, let’s learn how to find the cofactors of the elements in a $3 \times 3$ square matrix by the concept of the minors of entries in a three by three square matrix.

Cofactors of entries in First Row

The $e_{11}$, $e_{12}$ and $e_{13}$ are the entries in the first row of a $3 \times 3$ matrix $A$, and their corresponding cofactors are denoted by $C_{11}$, $C_{12}$ and $C_{13}$.

The $e_{11}$ is an entry in first row and first column of a $3×3$ matrix.

1. Find the minor of entry $e_{11}$ by leaving the entries in first row and first column.
2. The entry belongs to first row and first column. So, find the negative one raised to the power of sum of one and one.

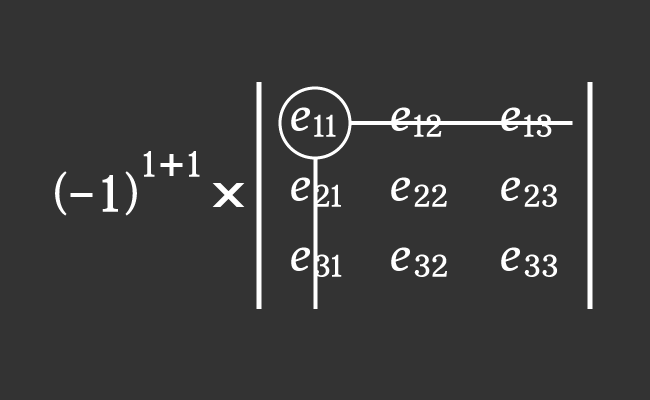
Now, calculate the product of the above two factors to find the cofactor $C_{11}$ mathematically.

$C_{11}$ $\,=\,$ $(-1)^{1+1} \times M_{11}$

$\implies$ $C_{11}$ $\,=\,$ $(-1)^{2} \times M_{11}$

$\implies$ $C_{11}$ $\,=\,$ $1 \times M_{11}$

$\implies$ $C_{11}$ $\,=\,$ $M_{11}$

$\implies$ $C_{11}$ $\,=\,$ $\begin{vmatrix} e_{22} & e_{23} \\ e_{32} & e_{33} \\ \end{vmatrix}$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{11}$ $\,=\,$ $e_{22} \times e_{33}$ $-$ $e_{32} \times e_{23}$

The $e_{12}$ is an element in first row and second column of a matrix of order $3$.

1. Calculate the minor of entry $e_{12}$ by leaving the elements in first row and second column.
2. The element belongs to first row and second column. For that reason, find the negative one raised to the power of sum of one and two.

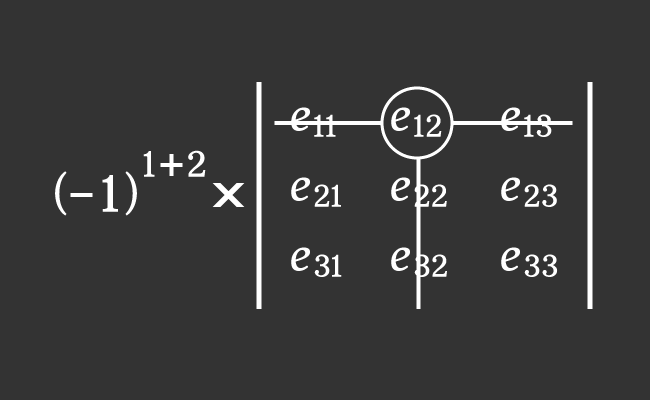
Now, evaluate the product of the above two factors to calculate the cofactor $C_{12}$ in mathematics.

$C_{12}$ $\,=\,$ $(-1)^{1+2} \times M_{12}$

$\implies$ $C_{12}$ $\,=\,$ $(-1)^{3} \times M_{12}$

$\implies$ $C_{12}$ $\,=\,$ $(-1) \times M_{12}$

$\implies$ $C_{12}$ $\,=\,$ $-M_{12}$

$\implies$ $C_{12}$ $\,=\,$ $-\begin{vmatrix} e_{21} & e_{23} \\ e_{31} & e_{33} \\ \end{vmatrix}$

$\implies$ $C_{12}$ $\,=\,$ $-(e_{21} \times e_{33}$ $-$ $e_{31} \times e_{23})$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{12}$ $\,=\,$ $e_{31} \times e_{23}$ $-$ $e_{21} \times e_{33}$

The $e_{13}$ is an entry in first row and third column of a $3×3$ matrix $A$.

1. Evaluate the minor of element $e_{13}$ by leaving the entries in first row and third column.
2. The entry belongs to first row and third column. Therefore, find the negative one raised to the power of sum of one and three.

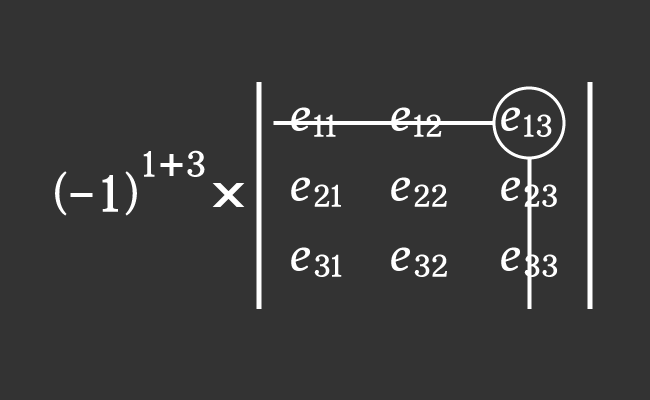
Now, calculate the product of the above two factors to find the cofactor $C_{13}$ in mathematics.

$C_{13}$ $\,=\,$ $(-1)^{1+3} \times M_{13}$

$\implies$ $C_{13}$ $\,=\,$ $(-1)^{4} \times M_{13}$

$\implies$ $C_{13}$ $\,=\,$ $1 \times M_{13}$

$\implies$ $C_{13}$ $\,=\,$ $M_{13}$

$\implies$ $C_{13}$ $\,=\,$ $\begin{vmatrix} e_{21} & e_{22} \\ e_{31} & e_{32} \\ \end{vmatrix}$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{13}$ $\,=\,$ $e_{21} \times e_{32}$ $-$ $e_{31} \times e_{22}$

Cofactors of elements in Second Row

The $e_{21}$, $e_{22}$ and $e_{23}$ are the elements in the second row of a matrix $A$, and the cofactors of them are denoted by $C_{21}$, $C_{22}$ and $C_{23}$ respectively.

The $e_{21}$ is an element in second row and first column of a matrix of order three.

1. Calculate the minor of element $e_{21}$ by leaving the entries in second row and first column.
2. The element belongs to second row and first column. For that reason, evaluate the negative one raised to the power of sum of two and one.

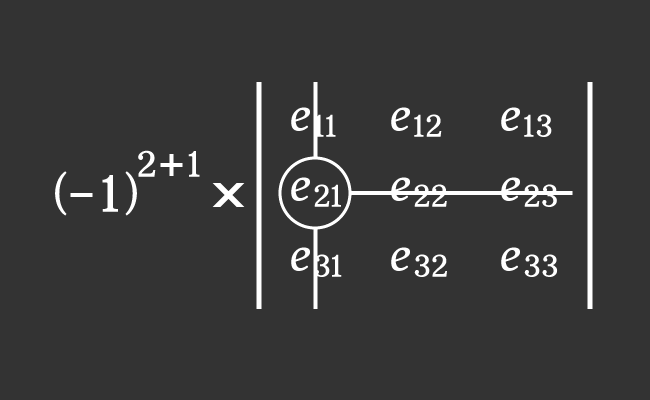
Now, find the product of the above two factors to evaluate the cofactor $C_{21}$ in mathematics.

$C_{21}$ $\,=\,$ $(-1)^{2+1} \times M_{21}$

$\implies$ $C_{21}$ $\,=\,$ $(-1)^{3} \times M_{21}$

$\implies$ $C_{21}$ $\,=\,$ $(-1) \times M_{21}$

$\implies$ $C_{21}$ $\,=\,$ $-M_{21}$

$\implies$ $C_{21}$ $\,=\,$ $-\begin{vmatrix} e_{12} & e_{13} \\ e_{32} & e_{33} \\ \end{vmatrix}$

$\implies$ $C_{21}$ $\,=\,$ $-(e_{12} \times e_{33}$ $-$ $e_{32} \times e_{13})$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{21}$ $\,=\,$ $e_{32} \times e_{13}$ $-$ $e_{12} \times e_{33}$

The $e_{22}$ is an entry in second row and second column of a $3 \times 3$ matrix $A$.

1. Evaluate the minor of entry $e_{22}$ by leaving the entries in second row and second column.
2. The entry belongs to second row and second column. Therefore, find the negative one raised to the power of sum of two and two.

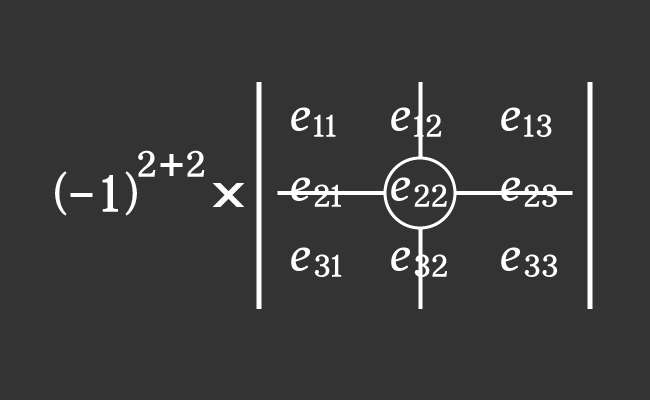
Now, find the product of the above two factors to find the cofactor $C_{22}$ mathematically.

$C_{22}$ $\,=\,$ $(-1)^{2+2} \times M_{22}$

$\implies$ $C_{22}$ $\,=\,$ $(-1)^{4} \times M_{22}$

$\implies$ $C_{22}$ $\,=\,$ $1 \times M_{22}$

$\implies$ $C_{22}$ $\,=\,$ $M_{22}$

$\implies$ $C_{22}$ $\,=\,$ $\begin{vmatrix} e_{11} & e_{13} \\ e_{31} & e_{33} \\ \end{vmatrix}$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{22}$ $\,=\,$ $e_{11} \times e_{33}$ $-$ $e_{31} \times e_{13}$

The $e_{23}$ is an element in second row and third column of a three by three matrix $A$.

1. Find the minor of element $e_{23}$ by leaving the elements in second row and third column.
2. The entry belongs to second row and third column. So, calculate the negative one raised to the power of sum of two and three.

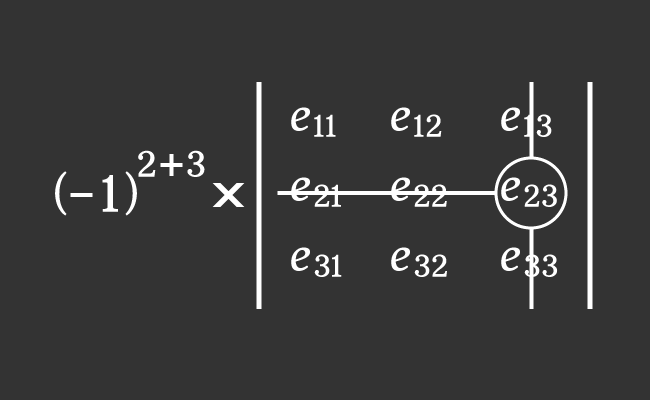
Now, evaluate the product of the above two factors to calculate the cofactor $C_{23}$ in mathematics.

$C_{23}$ $\,=\,$ $(-1)^{2+3} \times M_{23}$

$\implies$ $C_{23}$ $\,=\,$ $(-1)^{5} \times M_{23}$

$\implies$ $C_{23}$ $\,=\,$ $(-1) \times M_{23}$

$\implies$ $C_{23}$ $\,=\,$ $-M_{23}$

$\implies$ $C_{23}$ $\,=\,$ $-\begin{vmatrix} e_{11} & e_{12} \\ e_{31} & e_{32} \\ \end{vmatrix}$

$\implies$ $C_{23}$ $\,=\,$ $-(e_{11} \times e_{32}$ $-$ $e_{31} \times e_{12})$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{23}$ $\,=\,$ $e_{31} \times e_{12}$ $-$ $e_{11} \times e_{32}$

Cofactors of entries in Third Row

The $e_{31}$, $e_{32}$ and $e_{33}$ are the elements in the third row of a square matrix $A$ of order $3$, and the cofactors are denoted by $C_{31}$, $C_{32}$ and $C_{33}$ respectively.

The $e_{31}$ is an entry in third row and first column of a square matrix of order $3$.

1. Evaluate the minor of entry $e_{31}$ by leaving the elements in third row and first column.
2. The entry belongs to third row and first column. Therefore, evaluate the negative one raised to the power of sum of three and one.

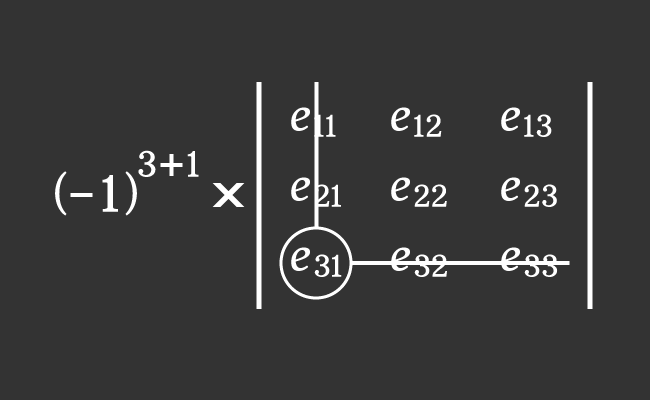
Now, evaluate the product of the above two factors to calculate the cofactor $C_{31}$ mathematically.

$C_{31}$ $\,=\,$ $(-1)^{3+1} \times M_{31}$

$\implies$ $C_{31}$ $\,=\,$ $(-1)^{4} \times M_{31}$

$\implies$ $C_{31}$ $\,=\,$ $1 \times M_{31}$

$\implies$ $C_{31}$ $\,=\,$ $M_{31}$

$\implies$ $C_{31}$ $\,=\,$ $\begin{vmatrix} e_{12} & e_{13} \\ e_{22} & e_{23} \\ \end{vmatrix}$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{31}$ $\,=\,$ $e_{12} \times e_{23}$ $-$ $e_{22} \times e_{13}$

The $e_{32}$ is an element in third row and second column of a $3 \times 3$ square matrix.

1. Find the minor of entry $e_{32}$ by leaving the entries in third row and second column.
2. The entry belongs to third row and second column. So, calculate the negative one raised to the power of sum of three and two.

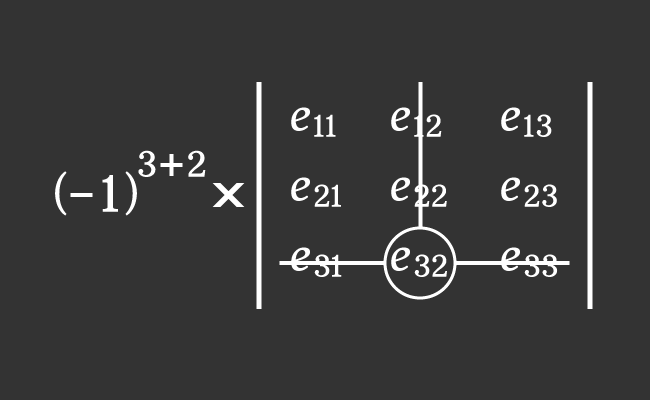
Now, find the product of the above two factors to find the cofactor $C_{32}$ mathematically.

$C_{32}$ $\,=\,$ $(-1)^{3+2} \times M_{32}$

$\implies$ $C_{32}$ $\,=\,$ $(-1)^{5} \times M_{32}$

$\implies$ $C_{32}$ $\,=\,$ $(-1) \times M_{32}$

$\implies$ $C_{32}$ $\,=\,$ $-M_{32}$

$\implies$ $C_{32}$ $\,=\,$ $-\begin{vmatrix} e_{11} & e_{13} \\ e_{21} & e_{23} \\ \end{vmatrix}$

$\implies$ $C_{32}$ $\,=\,$ $-(e_{11} \times e_{23}$ $-$ $e_{21} \times e_{13})$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{32}$ $\,=\,$ $e_{21} \times e_{13}$ $-$ $e_{11} \times e_{23}$

The $e_{33}$ is an element in third row and third column of a $3×3$ square matrix $A$.

1. Calculate the minor of entry $e_{33}$ by leaving the elements in third row and third column.
2. The element belongs to third row and third column. For that reason, evaluate the negative one raised to the power of addition of three and three.

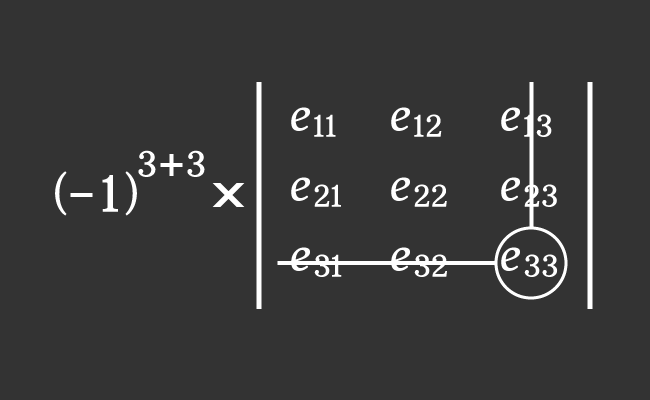
Now, evaluate the product of the above two factors to find the cofactor $C_{33}$ in mathematics.

$C_{33}$ $\,=\,$ $(-1)^{3+3} \times M_{33}$

$\implies$ $C_{33}$ $\,=\,$ $(-1)^{6} \times M_{33}$

$\implies$ $C_{33}$ $\,=\,$ $1 \times M_{33}$

$\implies$ $C_{33}$ $\,=\,$ $M_{33}$

$\implies$ $C_{33}$ $\,=\,$ $\begin{vmatrix} e_{11} & e_{12} \\ e_{21} & e_{22} \\ \end{vmatrix}$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{33}$ $\,=\,$ $e_{11} \times e_{22}$ $-$ $e_{21} \times e_{12}$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.