
Externally, some angles are formed geometrically when two or more nonparallel lines are intersected by their transversal line and the outer angles are called as exterior angles of nonparallel lines and their transversal.
Look at the picture which expresses intersection of two nonparallel lines and their transversal. In this case, four angles are formed externally and they are called as exterior angles of nonparallel lines and their transversal line.
When two nonparallel lines are cut by their transversal, four exterior angles are formed possibly in geometric system.
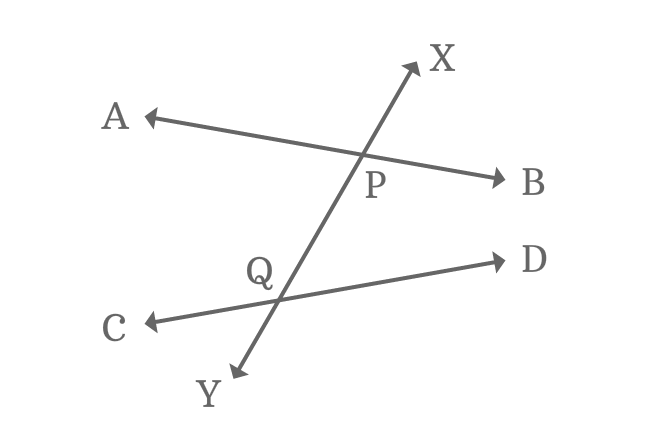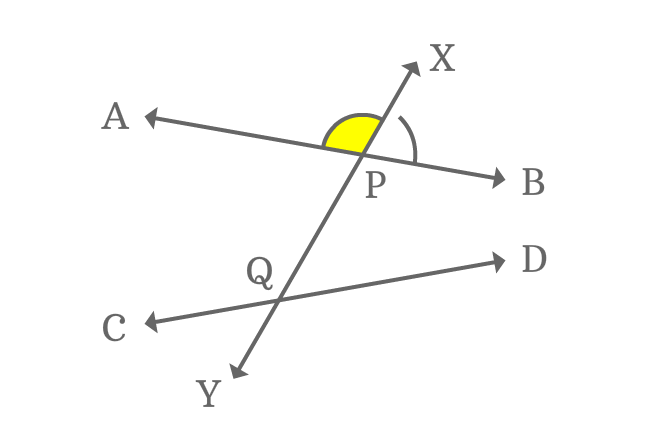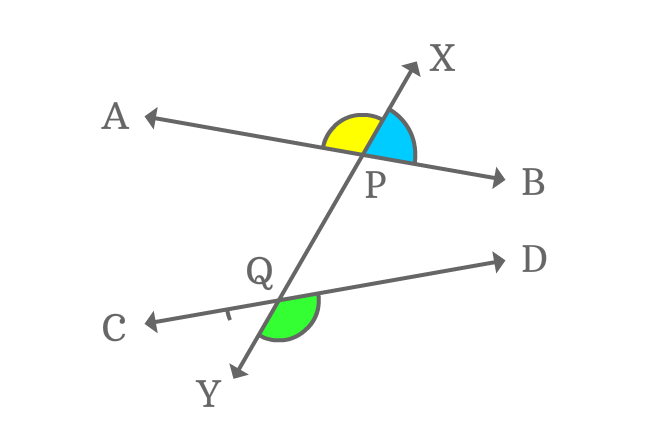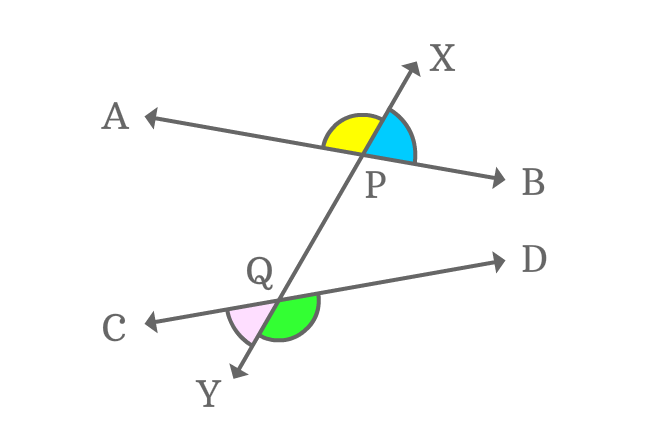
$1. \,\,\,\,\,\,$ $\angle APX$ is first external angle
$2. \,\,\,\,\,\,$ $\angle XPB$ is second external angle
$3. \,\,\,\,\,\,$ $\angle DQY$ is third external angle
$4. \,\,\,\,\,\,$ $\angle YQC$ is fourth external angle
The four angles are formed externally. So, they are known as exterior angles of nonparallel lines and their transversal.
All exterior angles are not equal when two nonparallel lines are cut by their transversal line. It is due to the non-parallelism of the intersecting lines.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2023 Math Doubts, All Rights Reserved