Evaluate $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{x}{\sqrt{x+4}-2}}$ by the Rationalization

The limit of $x$ divided by the square root of $x$ plus four minus two as the value of $x$ tends to zero should be evaluated in this limit problem by the rationalization.

$\implies$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{x}{\sqrt{x+4}-2}}$ $\,=\,$ $\dfrac{0}{0}$

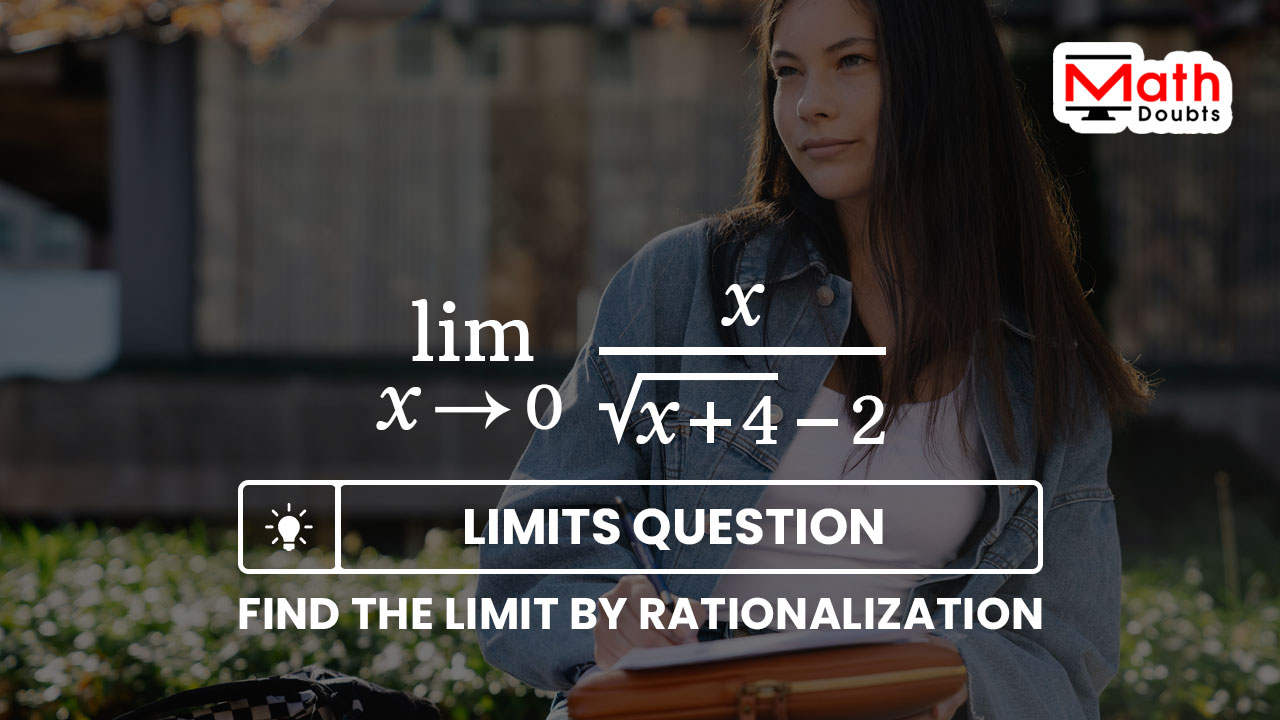
The limit by the direct substitution method is evaluated as indeterminate. So, let us find the limit of the irrational function $x$ divided by the square root of $x$ plus $4$ minus $2$ by the rationalisation.

Removal of indeterminate form by Rationalisation

The given function $x$ divided by square root of $x$ plus $4$ minus $2$ is a rational function basically but it becomes an irrational function due to the involvement of an irrational function the square root of $x$ plus $4$. Thus, the form of irrational function is the main reason for the indeterminate form.

However, it can be avoided by rationalizing the irrational form function by its conjugate function.

$=\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \bigg(\dfrac{x}{\sqrt{x+4}-2} \times 1\bigg)}$

In this irrational function, the expression $x$ in the numerator is not an irrational form function but expression in the denominator the square root of $x$ plus $4$ minus $2$ is an irrational function. So, it should be rationalized by multiplying the function with its conjugate function the square root of $x$ plus $4$ plus $2$.

$=\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \Bigg(\dfrac{x}{\sqrt{x+4}-2}}$ $\times$ $\dfrac{\sqrt{x+4}+2}{\sqrt{x+4}+2}\Bigg)$

Find the Product by Multiplying the functions

There are now two functions in fraction form inside the limit operation and the fractional functions are involved in multiplication. So, let’s find the product of them by the multiplication rule of the fractions.

$=\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \Bigg(\dfrac{x \times \big(\sqrt{x+4}+2\big)}{\big(\sqrt{x+4}-2\big) \times \big(\sqrt{x+4}+2\big)}\Bigg)}$

There is nothing to do in the numerator but there are two binomials with opposite signs in the denominator. It expresses the expansion of the difference of squares. So, it can be simplified by the difference of squares rule.

$=\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{x \times \big(\sqrt{x+4}+2\big)}{\big(\sqrt{x+4}\big)^2-2^2}}$

Now, let us concentrate on simplifying the irrational function.

$=\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{x \times \big(\sqrt{x+4}+2\big)}{x+4-4}}$

$=\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{x \times \big(\sqrt{x+4}+2\big)}{x+\cancel{4}-\cancel{4}}}$

$=\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{x \times \big(\sqrt{x+4}+2\big)}{x}}$

$=\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{\cancel{x} \times \big(\sqrt{x+4}+2\big)}{\cancel{x}}}$

$=\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \big(\sqrt{x+4}+2\big)}$

Find the Limit by the Direct substitution

The given irrational function is successfully simplified as the square root of $x$ plus $4$ plus $2$. Now, it is time to find the limit of square root of $x$ plus $4$ plus $2$ by the direct substitution method.

$=\,\,$ $\sqrt{0+4}+2$

$=\,\,$ $\sqrt{4}+2$

$=\,\,$ $2+2$

$=\,\,$ $4$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.