The distributive property of multiplication over subtraction can be proved in algebraic form by the geometrical method. Actually, it is derived in mathematics by the area of a rectangle.

Consider a rectangle but its dimensions are unknown. So, take the width and length of the rectangle as $a$ and $b$ respectively. Now, calculate the area of this rectangle in algebraic form.
$Area \,=\, a \times b$
$\implies$ $Area \,=\, a.b$
$\,\,\, \therefore \,\,\,\,\,\,$ $Area \,=\, ab$
Remember the area of this rectangle and it is used later in proving the distributive property.
Divide the rectangle across its length at a point as two different small rectangles.
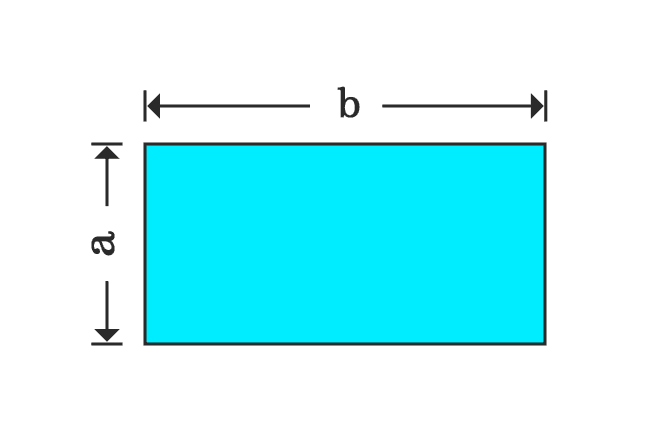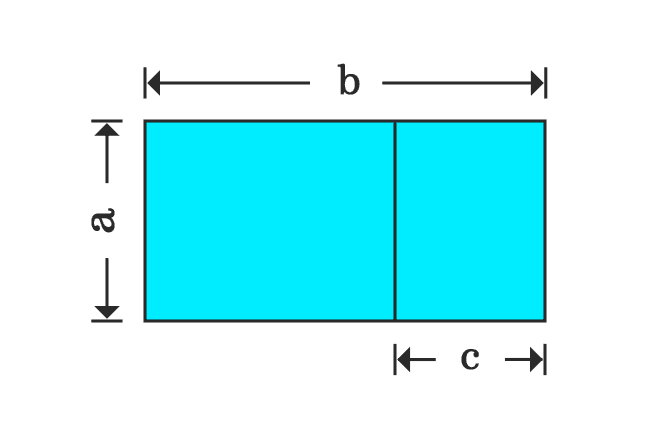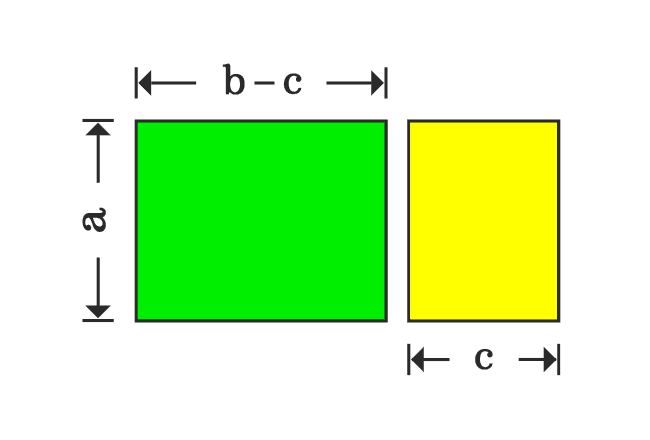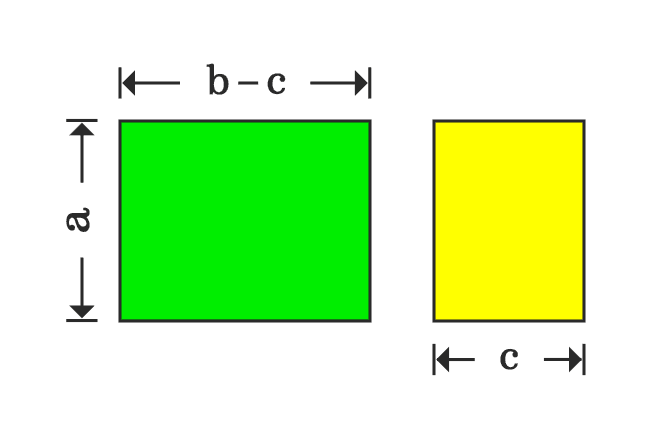
Calculate the area of first rectangle.
$Area \,=\, (b-c) \times a$
$\implies$ $Area \,=\, a \times (b-c)$
$\,\,\, \therefore \,\,\,\,\,\,$ $Area \,=\, a(b-c)$
Calculate the area of second rectangle.
$Area \,=\, c \times a$
$\implies$ $Area \,=\, a \times c$
$\,\,\, \therefore \,\,\,\,\,\,$ $Area \,=\, ac$
Geometrically, the first rectangle can be obtained by subtracting the second rectangle from the actual rectangle. So, the area first rectangle is equal to the subtraction of the area of second rectangle from the area of main rectangle.
$\,\,\, \therefore \,\,\,\,\,\,$ $a(b-c) \,=\, ab-ac$
You can derive it in another way if you are confused with the direct geometrical approach.
The area of the rectangle is $ab$ and it is divided as two rectangles whose areas $a(b-c)$ and $ac$. So, the area of the rectangle is equal to the sum of the areas of the small rectangles geometrically.
$ab$ $\,=\,$ $a(b-c)+ac$
According to Transposing method, the term $ac$ can be shifted to left-hand side of the equation from right-hand side.
$\implies$ $ab-ac \,=\, a(b-c)$
$\,\,\, \therefore \,\,\,\,\,\,$ $a(b-c) \,=\, ab-ac$
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2023 Math Doubts, All Rights Reserved