Cross multiplication method

Formula

$\dfrac{x}{b_{1}c_{2}-b_{2}c_{1}}$ $\,=\,$ $\dfrac{y}{c_{1}a_{2}-c_{2}a_{1}}$ $\,=\,$ $\dfrac{1}{a_{1}b_{2}-a_{2}b_{1}}$

Introduction

$a_1{x}+b_1{y}+c_1 = 0$ and $a_2{x}+b_2{y}+c_2 = 0$ are a system of linear equations in two variables $x$ and $y$. In this case, $a_1$, $a_2$, $b_1$ and $b_2$ are coefficients of $x$ and $y$. $c_1$ and $c_2$ are constants in the pair of linear equations in two variables. The values of $x$ and $y$ can be calculated from the following formulas.

$(1) \,\,\,$ $x \,=\, \dfrac{b_{1}c_{2}-b_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}$

$(2) \,\,\,$ $y \,=\, \dfrac{c_{1}a_{2}-c_{2}a_{1}}{a_{1}b_{2}-a_{2}b_{1}}$

In both formulas, $a_1b_2-a_2b_1$ is a denominator. If it is equal to zero, then the values of $x$ and $y$ become infinity. So, it should not be equal to zero.

$a_1b_2-a_2b_1 \,\ne\, 0$

$\implies$ $a_1b_2 \,\ne\, a_2b_1$

$\,\,\, \therefore \,\,\,\,\,\,$ $\dfrac{a_1}{a_2} \,\ne\, \dfrac{b_1}{b_2}$

Therefore, if $\dfrac{a_1}{a_2}$ is not equal to $\dfrac{b_1}{b_2}$, then the system of simultaneous linear equations has a unique solution.

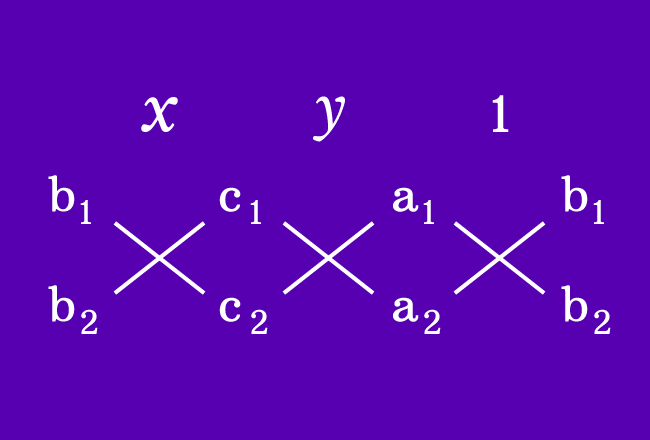
In this method, the values of $x$ and $y$ can be written as the following equations by cross multiplication.

$\implies$ $\dfrac{x}{b_{1}c_{2}-b_{2}c_{1}} \,=\, \dfrac{1}{a_{1}b_{2}-a_{2}b_{1}}$

$\implies$ $\dfrac{y}{c_{1}a_{2}-c_{2}a_{1}} \,=\, \dfrac{1}{a_{1}b_{2}-a_{2}b_{1}}$

$\,\,\, \therefore \,\,\,\,\,\,$ $\dfrac{x}{b_{1}c_{2}-b_{2}c_{1}}$ $\,=\,$ $\dfrac{y}{c_{1}a_{2}-c_{2}a_{1}}$ $\,=\,$ $\dfrac{1}{a_{1}b_{2}-a_{2}b_{1}}$

This formula can be remembered easily as displaying in the diagram.

Due to the involvement of cross multiplication technique for writing this equation, the method of solving $x$ and $y$ is called the cross multiplication method.

Proof

Learn how to derive the formulas for the cross multiplication method.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.