$\cot{(45^°)}$ Proof

Mathematically, the exact value of cot of $45$ degrees can be derived in three different methods. One of three methods is trigonometric approach but the remaining two methods are slightly different geometric methods. Study all of them here to know how to find the $\cot{(50^g)}$ value in trigonometry.

Theoretical approach

On the basis of direct relation between adjacent and opposite sides, the value of $\cot{\Big(\dfrac{\pi}{4}\Big)}$ is derived in mathematics in theoretical geometry method.

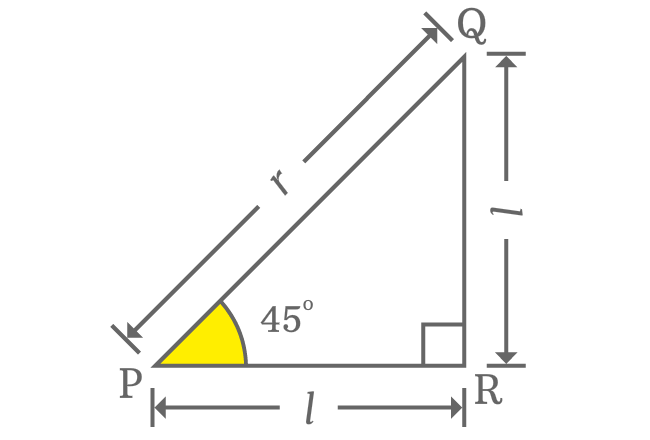
$\cot{(45^°)}$ $\,=\,$ $\dfrac{Length \, of \, Adjacent \, side}{Length \, of \, Opposite \, side}$

$\implies \cot{(45^°)} \,=\, \dfrac{PR}{QR}$

The lengths of adjacent and opposite sides are equal when angle of right triangle is $\dfrac{\pi}{4}$ radians. Therefore, the length of both opposite and adjacent sides is denoted by $l$ in this case.

$\implies \cot{(45^°)} \,=\, \dfrac{l}{l}$

$\implies \cot{(45^°)} \,=\, \require{cancel} \dfrac{\cancel{l}}{\cancel{l}}$

$\,\,\, \therefore \,\,\,\,\,\, \cot{(45^°)} \,=\, 1$

Practical approach

You can even find the exact value of cot of $\dfrac{\pi}{4}$ radians on your own by constructing a right triangle with $45$ degrees angle by using geometrical tools. Here, you are going to learn how to find it geometrically.

1. Draw a horizontal line from point $K$.
2. Coincide the point $K$ with the centre of a protractor and also coincide the horizontal line with right side base line of protractor. Then, mark a point at $45^°$ angle.
3. Draw a straight line from point $K$ through marked point of $\dfrac{\pi}{4}$ angle.
4. Set your compass to any length (for example $10 \, cm$) with ruler and draw an arc on $45^°$ angle line from point $K$. It intersects the $50^g$ angle line at point $L$.
5. Draw a perpendicular line to horizontal line from $L$ by the set square. It intersects the straight horizontal line at point $M$ and it forms a right angled triangle geometrically. It is denoted by $\Delta MKL$.

The $\Delta MKL$ is a right triangle with $45$ degrees angle. Now, let’s find the exact value of $\cot{(50^g)}$ from this triangle.

$\cot{(45^°)} = \dfrac{Length \, of \, Adjacent \, side}{Length \, of \, Opposite \, side}$

$\implies \cot{(45^°)} \,=\, \dfrac{KM}{LM}$

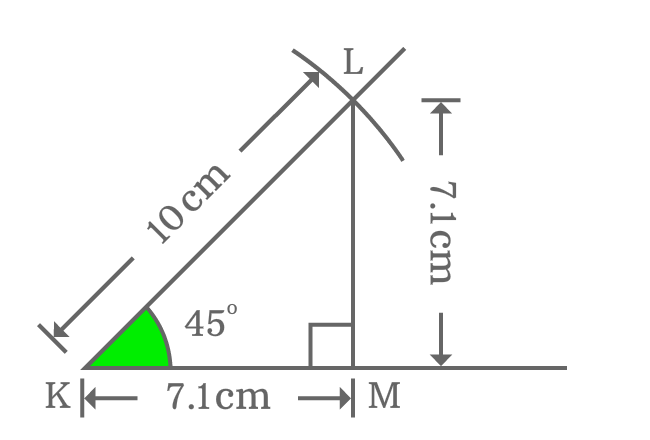
Actually, the lengths of adjacent and opposite sides are unknown but they can be measured by a ruler.

If you measure them by a ruler, you will be understood that the lengths of both adjacent side ($KM$) and opposite side ($LM$) are equal and the length of each side is equal to $7.1 \, cm$ approximately.

$\implies \cot{(45^°)} \,=\, \dfrac{KM}{LM} = \dfrac{7.1}{7.1}$

$\implies \cot{(45^°)} \,=\, \require{cancel} \dfrac{\cancel{7.1}}{\cancel{7.1}}$

$\,\,\, \therefore \,\,\,\,\,\, \cot{(45^°)} \,=\, 1$

Trigonometric approach

The value of cotangent of $45$ degrees can be exactly evaluated in trigonometry by the reciprocal identity of tan function.

$\cot{(45^°)} \,=\, \dfrac{1}{\tan{(45^°)}}$

Now, substitute the value of tan of $45$ degrees to get the $\cot{\Big(\dfrac{\pi}{4}\Big)}$ value.

$\implies \cot{(45^°)} \,=\, \dfrac{1}{1}$

$\,\,\, \therefore \,\,\,\,\,\, \cot{(45^°)} \,=\, 1$

Verdict

According to proofs of cot of $45$ degrees from above three methods, the exact value of $\cot{\Big(\dfrac{\pi}{4}\Big)}$ is equal to one.

Copyright © 2012 - 2022 Math Doubts, All Rights Reserved