Proof of $\cos{(36^°)}$ value

The exact value of cos 36 degrees in fraction is equal to the quotient of square root of five plus one by four.

$\cos{(36^°)}$ $\,=\,$ $\dfrac{\sqrt{5}+1}{4}$

The cosine of angle thirty six degrees can be derived mathematically in two different mathematical approaches. So, let’s learn each method to derive the cos of angle pi by five radian value.

Trigonometric method

In trigonometry, the exact value of cosine of angle thirty six degrees can be derived mathematically in fraction form on the basis of the sin 18 degrees value. So, it is essential to know for evaluating the cosine at angle pi by five radian.

Express the cos function in sine function

According to the trigonometry, the cos double angle identity can be used to express the cosine of double angle function in sine.

$\cos{(2\theta)}$ $\,=\,$ $1-2\sin^2{\theta}$

Now, take $\theta \,=\, 18^°$, and then $2\theta \,=\, 36^°$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $1-2\sin^2{(18^°)}$

Now, substitute the value of sine of angle eighteen degrees in the cos double angle formula.

$\implies$ $\cos{(36^°)}$ $\,=\,$ $1-2\Bigg(\dfrac{\sqrt{5}-1}{4}\Bigg)^2$

Simplify the Trigonometric equation

The cos of angle forty grades can be evaluated by simplifying the right hand side expression of the equation. The simplification process can be started by the power rule of a quotient.

$\implies$ $\cos{(36^°)}$ $\,=\,$ $1-2\Bigg(\dfrac{(\sqrt{5}-1)^2}{4^2}\Bigg)$

Look at the square of a binomial in the numerator of the second term of the expression. It can be expanded by the square of difference formula.

$\implies$ $\cos{(36^°)}$ $\,=\,$ $1-2\Bigg(\dfrac{(\sqrt{5})^2+(1)^2-2 \times (\sqrt{5}) \times 1}{16}\Bigg)$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $1-2\Bigg(\dfrac{5+1-2\sqrt{5}}{16}\Bigg)$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $1-2\Bigg(\dfrac{6-2\sqrt{5}}{16}\Bigg)$

The numerator of the second term of the right hand side expression of the equation can be simplified further by taking common factor out from the terms.

$\implies$ $\cos{(36^°)}$ $\,=\,$ $1-2\Bigg(\dfrac{2 \times 3-2\sqrt{5}}{16}\Bigg)$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $1-2\Bigg(\dfrac{2 \times (3-\sqrt{5})}{16}\Bigg)$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $1-\dfrac{2 \times 2 \times (3-\sqrt{5})}{16}$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $1-\dfrac{4 \times (3-\sqrt{5})}{16}$

$\implies \require{cancel}$ $\cos{(36^°)}$ $\,=\,$ $1-\dfrac{\cancel{4} \times (3-\sqrt{5})}{\cancel{16}}$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $1-\dfrac{3-\sqrt{5}}{4}$

Now, use the subtraction of fractions to simplify the right hand side expression of the equation.

$\implies$ $\cos{(36^°)}$ $\,=\,$ $\dfrac{1 \times 4 -(3-\sqrt{5})}{4}$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $\dfrac{4-(3-\sqrt{5})}{4}$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $\dfrac{4-3+\sqrt{5}}{4}$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $\dfrac{1+\sqrt{5}}{4}$

$\,\,\,\therefore\,\,\,\,\,\,$ $\cos{(36^°)}$ $\,=\,$ $\dfrac{\sqrt{5}+1}{4}$

In this way, the cos of thirty six degrees value can be evaluated in fraction form exactly in trigonometric approach.

Geometric method

The cosine of angle thirty six degrees value can be derived geometrically by constructing a right triangle with an angle thirty six degrees but it is not possible to evaluate the cos value exactly due to the problem of approximation. However, it can be derived approximately.

construction of right triangle for cos 36 degrees

Take a ruler and draw a horizontal line of any length. Here, $8\,cm$ straight line is drawn horizontally from the point $E$ to $F$.
Coincide the point $E$ with middle point of protractor and also coincide its right side base line with horizontal line, and then mark a point at $36^°$ angle. Later, draw a straight line from point $E$ through the marked point.
Finally, draw an intersecting line to $36^°$ angle line from point $F$ but it should be perpendicular to the horizontal line. Assume that it intersects the $36^°$ angle line at point $G$.

In this way, a right angled triangle, denoted by $\Delta FEG$ can be constructed geometrically with an angle thirty six degrees. Now, we have to evaluate the cosine of angle pi by five radian value from this triangle.

According to the fundamental definition of the cosine, it can be written in ratio of the sides of the triangle. In the $\Delta FEG$, the adjacent side is $\overline{EF}$ and hypotenuse is $\overline{EG}$.

$\cos{(36^°)}$ $\,=\,$ $\dfrac{EF}{EG}$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $\dfrac{8}{EG}$

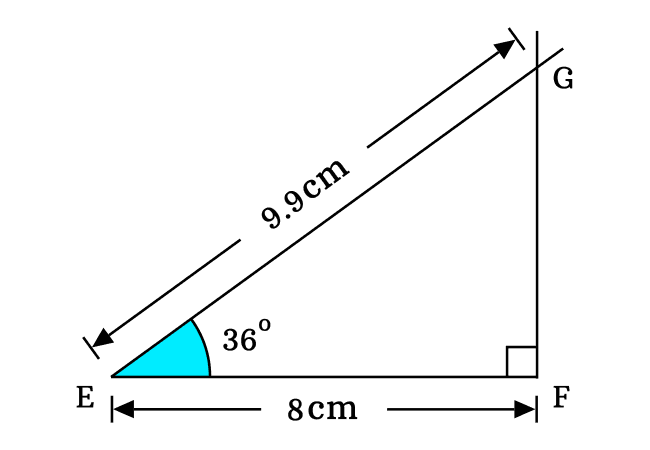
right angled triangle for cos 36 degrees

Here, we don’t know the length of the hypotenuse $\overline{EG}$ and it is not possible to evaluate the cos of thirty six degrees without the length of this side. Hence, take a ruler and measure the length of the hypotenuse. The length of the hypotenuse is approximately $9.9\,cm$ in this case.

$\implies$ $\cos{(36^°)}$ $\,=\,$ $\dfrac{8}{9.9}$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $0.8080808080\cdots$

$\,\,\,\therefore\,\,\,\,\,\,$ $\cos{(36^°)}$ $\,\approx\,$ $0.8081$

Conclusion

According to the trigonometric approach, the cosine of angle pi by five radian is derived in fraction form as follows.

$\cos{(36^°)}$ $\,=\,$ $\dfrac{\sqrt{5}+1}{4}$

$\implies$ $\cos{(36^°)}$ $\,=\,$ $0.8090169943\cdots$

$\implies$ $\cos{(36^°)}$ $\,\approx\,\,$ $0.809$

According to the geometrical approach, the cosine of angle forty grades is derived in decimal form as follows.

$\cos{(36^°)}$ $\,\approx\,$ $0.8081$

The cosine of thirty six degrees is $0.809$ in trigonometric method but it is $0.8081$ in geometrical approach.

$0.809-0.8081 \,=\, 0.0009$

$\implies$ $0.809-0.8081 \,\approx\, 0$

There is some difference between values of cos of forty grades but it is proved above that they are equal approximately because the difference between them is negligible. However, we should not take $0.8081$ as the value of cos of angle thirty six degrees because we have measured the length of hypotenuse approximately in the geometric method.

Therefore, we can take $0.809$ as the value of $\cos{\Big(\dfrac{\pi}{5}\Big)}$ because it is evaluated from the exact value in fraction form of the cos of thirty six degrees.