Constant

A quantity that does not change in any case is called a constant.

Introduction

The true meaning of constant is unchangeable. So, a constant is an unchangeable quantity in mathematics and it is usually represented by a literal algebraically.

There are some great mathematicians who used the concept of constant to denote some special quantities by some special literals and they are recognized globally by their special symbols.

Examples

There are several examples for the concept of a constant. Some of them are defined by mathematicians and remaining are user defined. Now, learn both of them here.

User defined constants

1. Number of days of a week

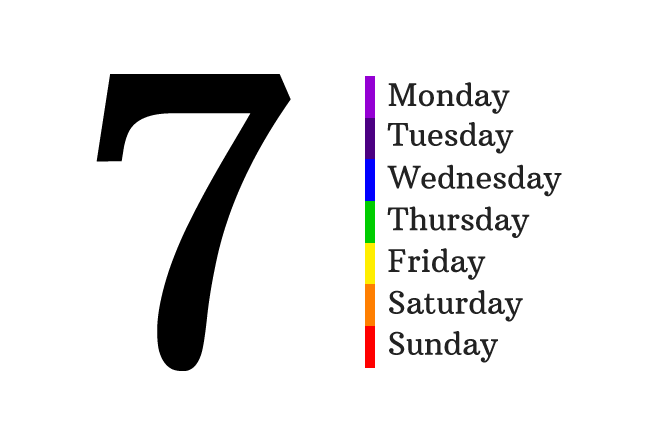
The total number of days of a week is $7$. It is same in all countries and also same in all years. It is not influenced by any situation. So, the number of days a week is constant.

It can be represented by symbol. For example, $w$.

$w \,=\, 7$

It is a user defined constant and it can be used everywhere to represent the total number of days of a week by the literal $w$ in mathematics.

2. Mass of Earth

The mass of earth is $5.97237 \times 10^{24} \, kg$

It is constant all the time and no factor chances it. But it is neither easy to remember nor easy to speak out every time. So, it is a good idea to represent it by a constant.

Let’s represent this quantity by a constant and it is assumed to denote by $m_{e}$.

$m_{e} \,=\, 5.97237 \times 10^{24} \, kg$

Now, just represent mass of earth by $m_{e}$ wherever you want to express it.

Thus, you can represent any constant quantity in mathematics by a user defined mathematical constant.

Globally Recognized constants

There are numerous user defined mathematical constants in which some of them are globally recognized by their special symbols. Here is some of globally recognized mathematical constants to understand the purpose of defining constants in mathematics.

1. Neper Constant

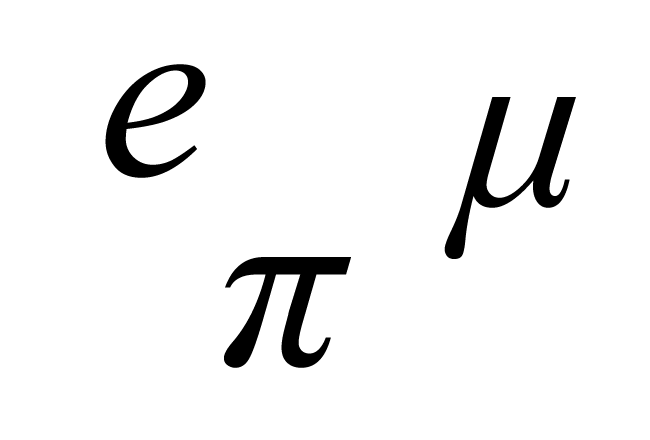
John Napier introduced a mathematical constant ($e$) to find the logarithm of any quantity on the basis of an irrational number.

$e \,=\, 2.7182818284\ldots$

2. Micro

A Greek symbol micro $(\mu)$ is used to represent the constant millionth.

$\mu \,=\, 0.000001$ $\,=\,$ $10^{-6}$ $\,=\,$ $\dfrac{1}{1000000}$

3. Pi

The ratio of circumference to diameter of a circle is a constant and an irrational number. It is represented by a special symbol ($\pi$).

$\pi \,=\, 3.1415926535\ldots$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.