Cofactors of a 2×2 Matrix

Each minor of a two by two matrix with a sign is called the cofactor of an entry in a square matrix of the order two.

Introduction

In a two by two matrix, the cofactor of an entry is calculated by multiplying the following two factors.

1. The negative one raised to the power of sum of the number of the row and the number of the column of the corresponding element.
2. The minor of the respective entry.

Let us learn how to find the cofactor of every entry for the following example matrix.

$B$ $\,=\,$ $\begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ \end{bmatrix}$

It is essential to learn how to find the minors of entries in a square matrix of the order two.

Cofactor of an entry in the first row and the first column

$b_{11}$ is the entry in the first row and the first column. Now, find the minor of this element.

$M_{11} \,=\, \begin{vmatrix} b_{22} \\ \end{vmatrix}$

$\therefore \,\,\,$ $M_{11} \,=\, b_{22}$

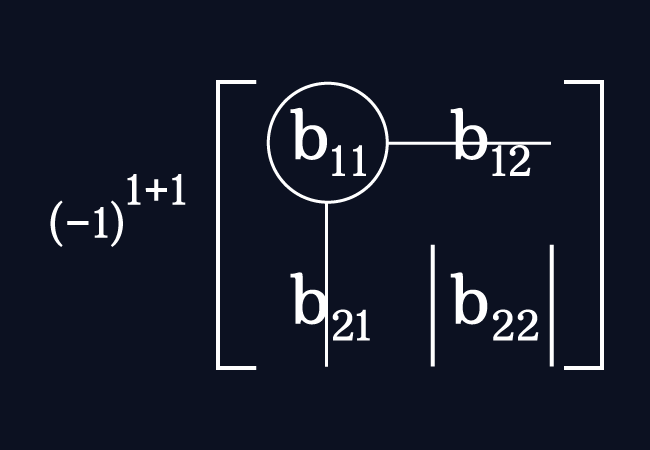
The cofactor of the element $b_{11}$ is denoted by $C_{11}$. For the element $b_{11}$, the number of the row is $1$ and the number of the column is $1$.

The cofactor of the entry $b_{11}$ is calculated by multiplying the minor of this entry with the negative one raised to the power of the sum of $1$ and $1$.

$C_{11} \,=\, (-1)^{1+1} \times M_{11}$

$\implies$ $C_{11} \,=\, (-1)^{1+1} \times b_{22}$

$\implies$ $C_{11} \,=\, (-1)^{2} \times b_{22}$

$\implies$ $C_{11} \,=\, 1 \times b_{22}$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{11} \,=\, b_{22}$

Therefore, the cofactor of the element $b_{11}$ in the matrix $B$ is positive $b_{22}$.

Cofactor of an entry in the first row and the second column

$b_{12}$ is the entry at the first row and the second column. Now, let’s find the minor of this element.

$M_{12} \,=\, \begin{vmatrix} b_{21} \\ \end{vmatrix}$

$\therefore \,\,\,$ $M_{12} \,=\, b_{21}$

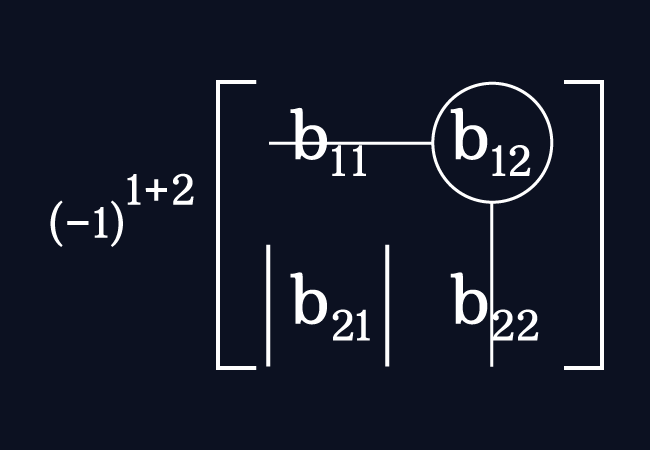
The cofactor of the element $b_{12}$ is denoted by $C_{12}$. For the element $b_{12}$, the number of the row is $1$ and the number of the column is $2$.

The cofactor of the entry $b_{12}$ is evaluated by multiplying the minor of this element with the negative one raised to the power of the sum of $1$ and $2$.

$C_{12} \,=\, (-1)^{1+2} \times M_{12}$

$\implies$ $C_{12} \,=\, (-1)^{1+2} \times b_{21}$

$\implies$ $C_{12} \,=\, (-1)^{3} \times b_{21}$

$\implies$ $C_{12} \,=\, (-1) \times b_{21}$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{12} \,=\, -b_{21}$

Therefore, the cofactor of the element $b_{12}$ in the matrix $B$ is negative $b_{21}$.

Cofactor of an entry in the second row and the first column

$b_{21}$ is the entry at the second row and the first column. Now, let us evaluate the minor of this entry.

$M_{21} \,=\, \begin{vmatrix} b_{12} \\ \end{vmatrix}$

$\therefore \,\,\,$ $M_{21} \,=\, b_{12}$

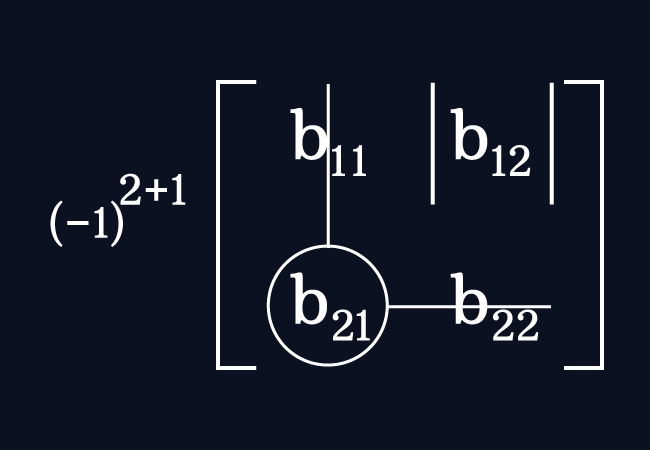
The cofactor of the element $b_{21}$ is denoted by $C_{21}$. For the entry $b_{21}$, the number of the row is $2$ and the number of the column is $1$.

The cofactor of the entry $b_{21}$ is evaluated by multiplying the minor of this element with the negative one raised to the power of the sum of $2$ and $1$.

$C_{21} \,=\, (-1)^{2+1} \times M_{21}$

$\implies$ $C_{21} \,=\, (-1)^{2+1} \times b_{12}$

$\implies$ $C_{21} \,=\, (-1)^{3} \times b_{12}$

$\implies$ $C_{21} \,=\, (-1) \times b_{12}$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{21} \,=\, -b_{12}$

Therefore, the cofactor of the entry $b_{21}$ in the matrix $B$ is negative $b_{12}$.

Cofactor of an entry in the second row and the second column

$b_{22}$ is the entry in the second row and the second column. Now, let us evaluate the minor of this entry.

$M_{22} \,=\, \begin{vmatrix} b_{11} \\ \end{vmatrix}$

$\therefore \,\,\,$ $M_{22} \,=\, b_{11}$

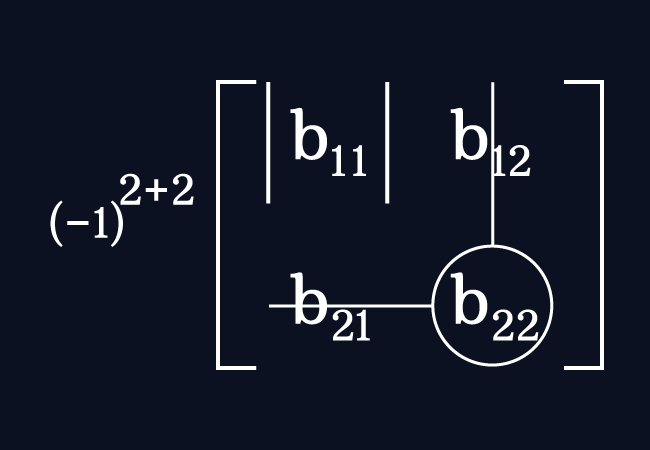
The cofactor of the element $b_{22}$ is represented by $C_{22}$. For the entry $b_{22}$, the number of the row is $2$ and the number of the column is $2$.

The cofactor of the entry $b_{22}$ is calculated by multiplying the minor of this entry with the negative one raised to the power of the sum of $2$ and $2$.

$C_{22} \,=\, (-1)^{2+2} \times M_{22}$

$\implies$ $C_{22} \,=\, (-1)^{2+2} \times b_{11}$

$\implies$ $C_{22} \,=\, (-1)^{4} \times b_{11}$

$\implies$ $C_{22} \,=\, 1 \times b_{11}$

$\,\,\,\therefore\,\,\,\,\,\,$ $C_{22} \,=\, b_{11}$

Therefore, the cofactor of the element $b_{22}$ in the matrix $B$ is positive $b_{11}$.

Signs

A sign technique can be used as a shortcut method while finding the cofactors of entries in a $2 \times 2$ matrix.

$B$ $\,=\,$ $\begin{bmatrix} + & – \\ b_{11} & b_{12} \\ – & + \\ b_{21} & b_{22} \\ \end{bmatrix}$

1. In the first row, write a plus sign above the first element and a negative sign over the second element.
2. In the second row, write a minus sign above the first element and a positive sign over the second element.

Now, let’s find the cofactors of the elements for the above matrix.

1. $C_{11} \,=\, +M_{11} \,=\, +\begin{vmatrix} b_{22} \\ \end{vmatrix} \,=\, b_{22}$
2. $C_{12} \,=\, -M_{12} \,=\, -\begin{vmatrix} b_{21} \\ \end{vmatrix} \,=\, -b_{21}$
3. $C_{21} \,=\, -M_{21} \,=\, -\begin{vmatrix} b_{12} \\ \end{vmatrix} \,=\, -b_{12}$
4. $C_{22} \,=\, +M_{22} \,=\, +\begin{vmatrix} b_{11} \\ \end{vmatrix} \,=\, b_{11}$

Remember that this shortcut method is recommendable to use for verifying our fundamental process and also to get the result quickly.

Example

$A$ $\,=\,$ $\begin{bmatrix} 5 & 3 \\ -2 & 6 \\ \end{bmatrix}$

Let’s find the cofactors of the entries in the the matrix $A$ of the order $2$.

$(1).\,\,\,$ $C_{11} \,=\, (-1)^{1+1}\begin{vmatrix} 6 \\ \end{vmatrix} \,=\, +\begin{vmatrix} 6 \\ \end{vmatrix} \,=\, 6$

The cofactor of the entry five is positive six.

$(2).\,\,\,$ $C_{12} \,=\, (-1)^{1+2}\begin{vmatrix} -2 \\ \end{vmatrix} \,=\, -\begin{vmatrix} -2 \\ \end{vmatrix} \,=\, -(-2)$ $\,=\,$ $2$

The cofactor of the entry three is positive two.

$(3).\,\,\,$ $C_{21} \,=\, (-1)^{2+1}\begin{vmatrix} 3 \\ \end{vmatrix} \,=\, -\begin{vmatrix} 3 \\ \end{vmatrix} \,=\, -3$

The cofactor of the entry negative two is negative three.

$(4).\,\,\,$ $C_{22} \,=\, (-1)^{2+2}\begin{vmatrix} 6 \\ \end{vmatrix} \,=\, +\begin{vmatrix} 5 \\ \end{vmatrix} \,=\, 5$

The cofactor of the entry six is positive five.

In this way, the cofactor of every element can be calculated in a square matrix of the order two.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.