Belongs to

A symbol that expresses the phrase “to be a member of” in the set theory is called the belongs to symbol.

Introduction

In the set theory, the elements (or members) are collected on the basis of one or more common properties to form a set. So, each element is a member of that set. Hence, it is simply expressed as the element belongs to the set.

An Italian mathematician, Giuseppe Peano used a Greek letter lunate epsilon ($∈$) for expressing the phrase “belongs to” symbolically in set theory. It helps us to express the relationship between an element and its set in mathematical form.

Usage

Let’s learn how to use the symbol epsilon in set theory from two understandable examples.

Basic example

The numbers $0$, $2$, $5$, $8$ and $9$ are collected to form a set $N$ in this example.

The number $0$ is a member of set $N$. Hence, it is expressed as $0 \,∈\, N$.
The number $2$ is an element of set $N$. So, it is written as $2 \,∈\, N$.
The number $5$ belongs to set $N$. Therefore, the relationship between them is written as $5 \,∈\, N$.
The number $8$ is in set $N$ and it is expressed as $8 \,∈\, N$.
The number $9$ lies in set $N$ and it is written as $9 \,∈\, N$.

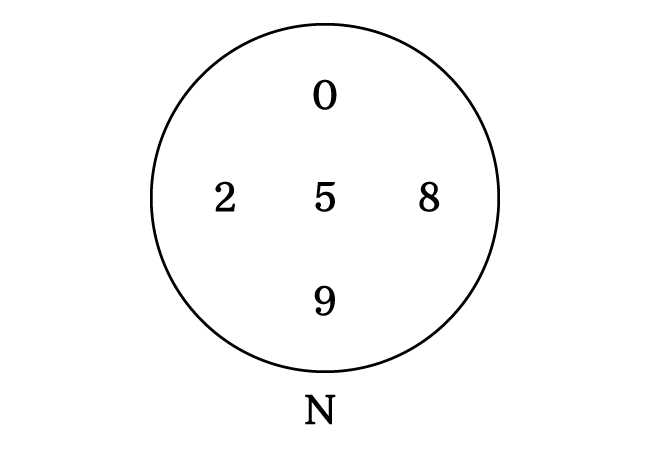
Thus, we use the epsilon symbol in set theory to express the relationship between an element and a set in mathematical form.

Advanced example

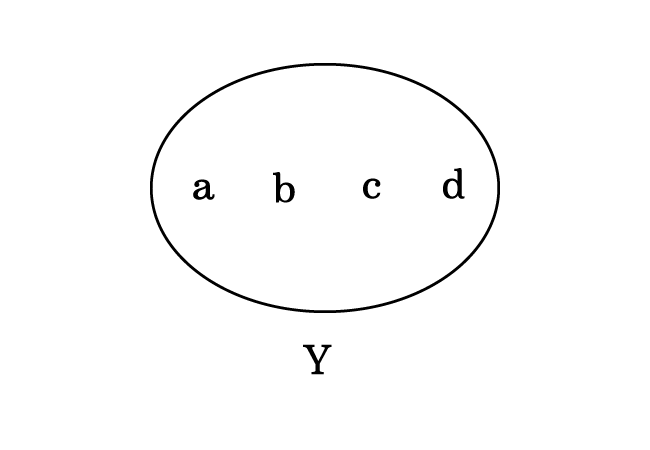
The lowercase letters $a$, $b$, $c$ and $d$ are collected to form a set $Y$ in this example.

The letter $a$ is a member of set $Y$. Hence, it is expressed as $a \,∈\, Y$.
The letter $b$ is an element of set $Y$. So, it is written as $b \,∈\, Y$.
The letter $c$ belongs to set $Y$. Therefore, the relationship between them is written as $c \,∈\, Y$.
The letter $d$ is in set $Y$ and it is expressed as $d \,∈\, Y$.