A fraction whose quantity is greater than or equal to whole quantity is called an improper fraction.
The meaning of improper fraction is defined from the meanings of the words “Improper” and “Fraction”.
As per the meanings of them, it is not acceptable to consider either a whole quantity or the sum of a whole quantity and a part of another whole quantity as a fraction. So, the unacceptable fraction is called as an improper fraction.
According to the theory of the improper fraction.
The quantity of an improper fraction is called by comparing its quantity of total number of selected parts with the number of parts of a whole quantity. It’s actually done by the ratio in mathematics.
$Number \, of \, Selected \, parts$ $\,\geq\,$ $Total \, number \, of \, Parts \, of \, a \, Quantity$
$\implies$ $\dfrac{Number \, of \, Selected \, parts}{Total \, number \, of \, Parts \, of \, a \, Quantity}$ $\,\geq\,$ $1$
$\,\,\, \therefore \,\,\,\,\,\,$ $Improper \, fraction$ $\,=\,$ $\dfrac{Number \, of \, Selected \, parts}{Total \, number \, of \, Parts \, of \, a \, Quantity}$ $\,\geq\,$ $1$
An improper fraction is completely opposite to the proper fraction. The following examples help you to understand how fractions are formed improperly.
Consider a circle and split it as three equal parts. Now, let’s calculate the improper fraction mathematically.
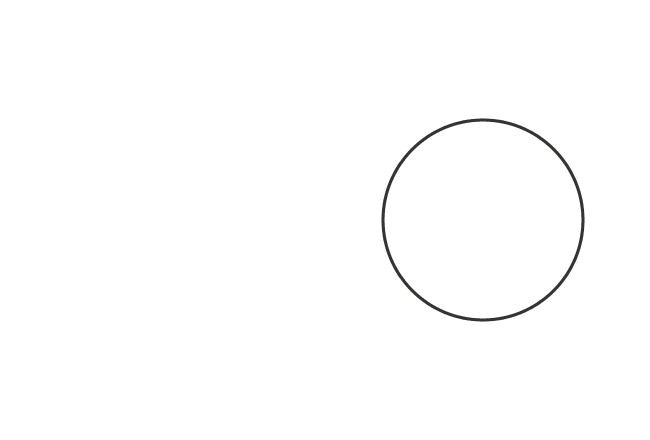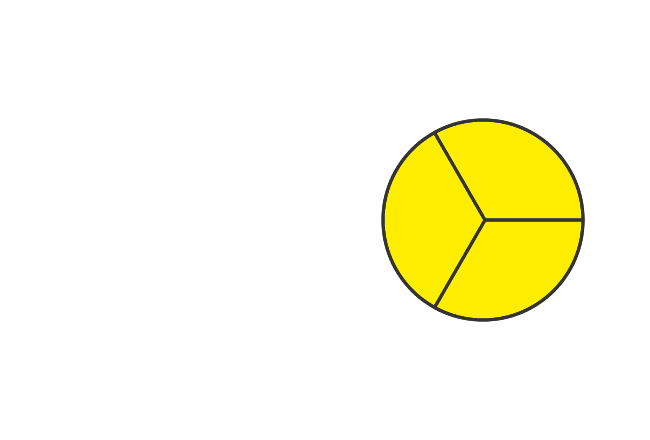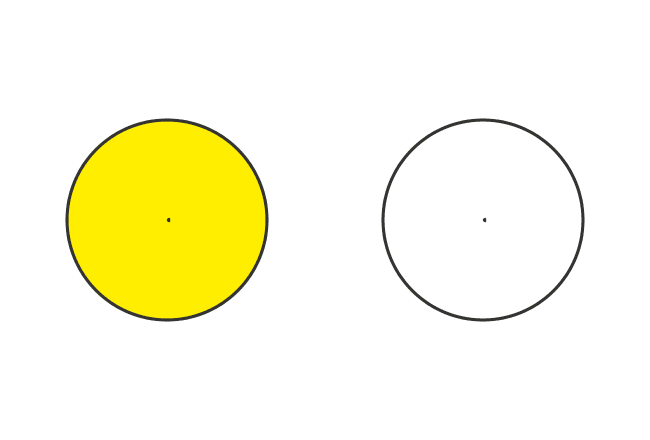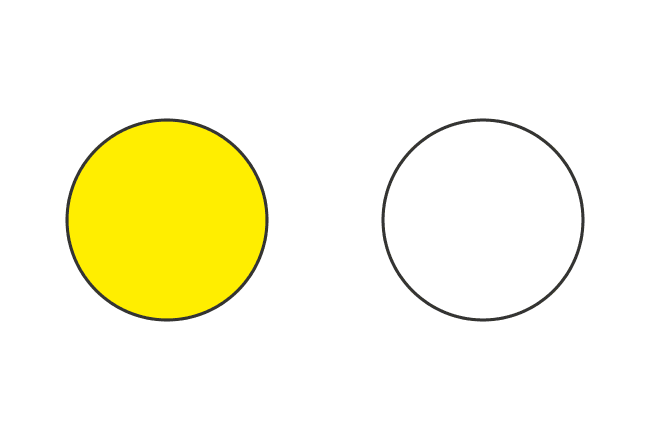
The total number of parts of a circle is $3$, take all three parts and then evaluate the fraction.
Fraction $\,=\, \dfrac{3}{3}$
$\implies$ Fraction $\,=\, \require{cancel} \dfrac{\cancel{3}}{\cancel{3}}$
$\,\,\, \therefore \,\,\,\,\,\,$ Fraction $\,=\, 1$
It is calculated that the fraction $\dfrac{3}{3}$ is equal to $1$ but the number $1$ is an integer and it represents a whole quantity.
So, it is not proper to consider $\dfrac{3}{3}$ as a fraction. Therefore, the fraction $\dfrac{3}{3}$ or $1$ is called an improper fraction. It is proved that any positive integer or a whole number is called as an improper fraction.
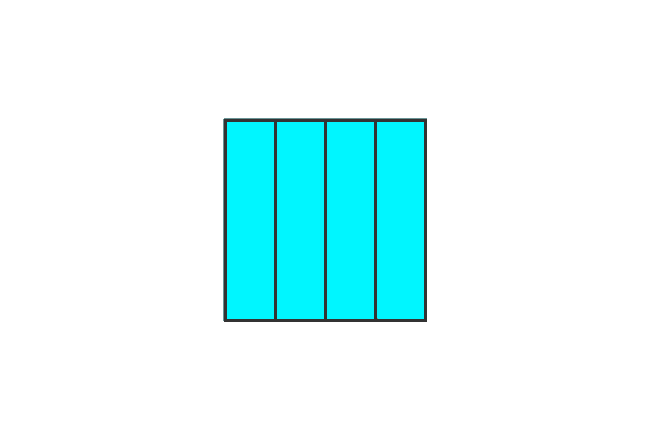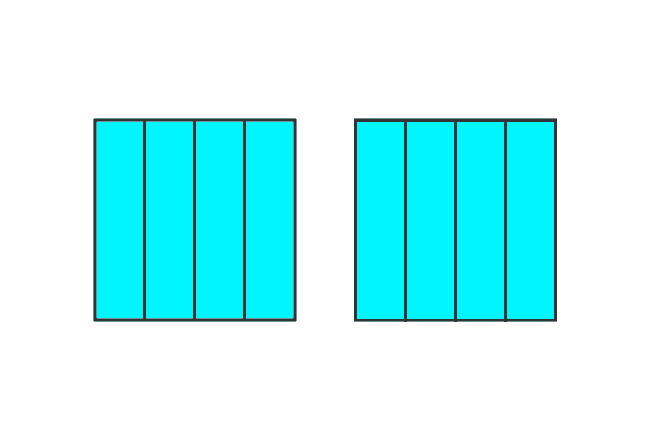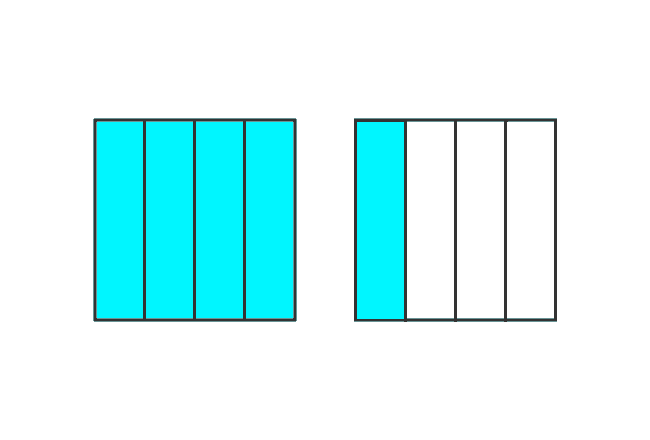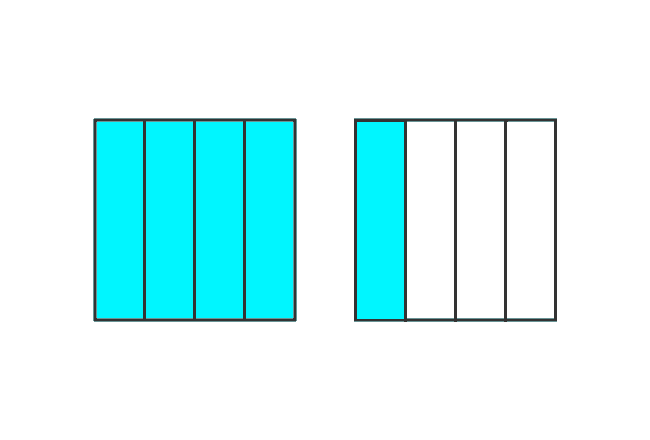
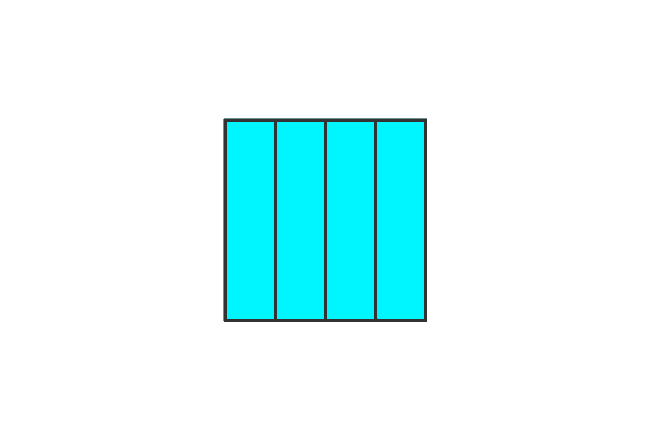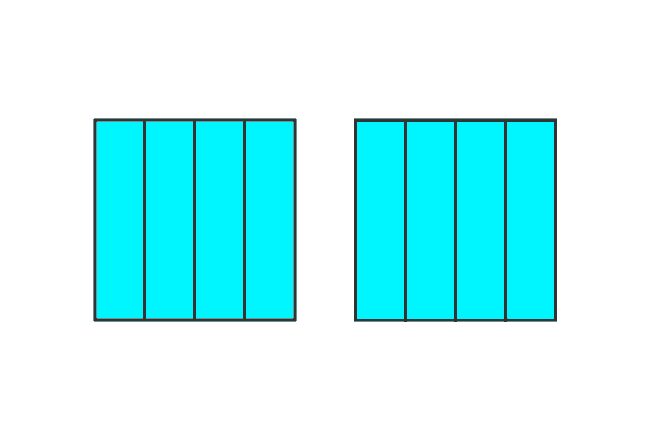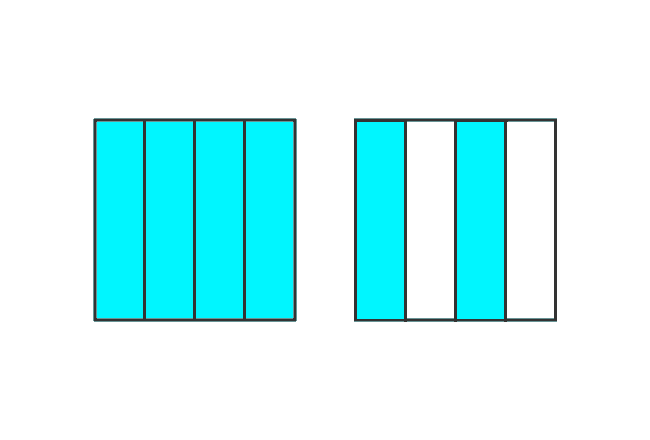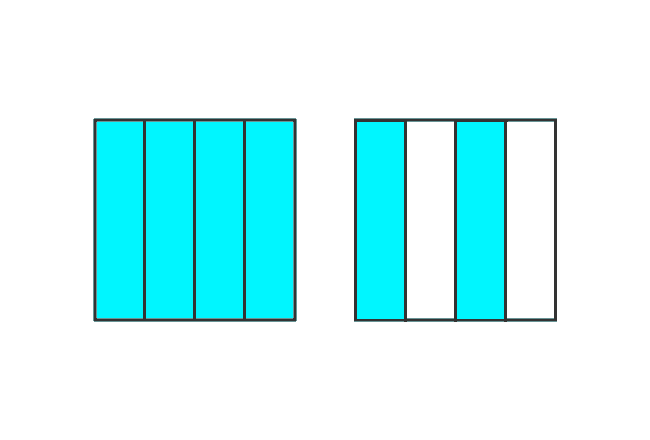
Consider two squares. Take, all parts from one square and a part from another square.
Fraction = $\dfrac{4}{4} + \dfrac{1}{4}$ = $\dfrac{5}{4}$
It is written as $5 : 4$ in ratio form. In this case, the value of numerator is greater than its denominator ($5 > 4$). Therefore, it’s known as an improper fraction.
Improper fraction = $\dfrac{5}{4}$
Take, all parts from one square and two parts from another square.
Fraction = $\dfrac{4}{4} + \dfrac{2}{4}$ = $\dfrac{6}{4}$
It’s written as $6 : 4$ in ratio form. The value in the numerator is greater than its denominator ($6 > 4$). So, it’s considered as an improper fraction.
Improper fraction = $\dfrac{6}{4}$
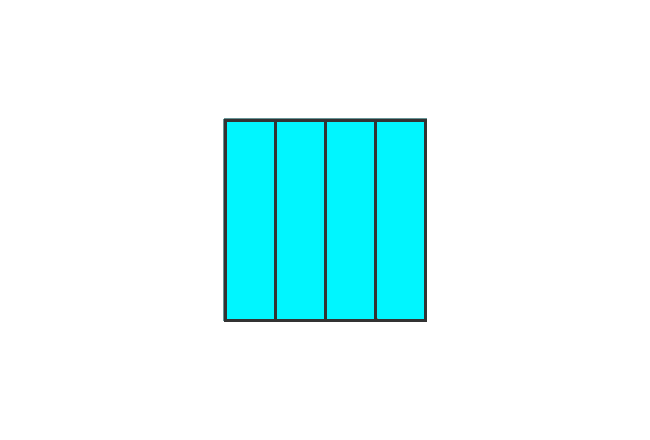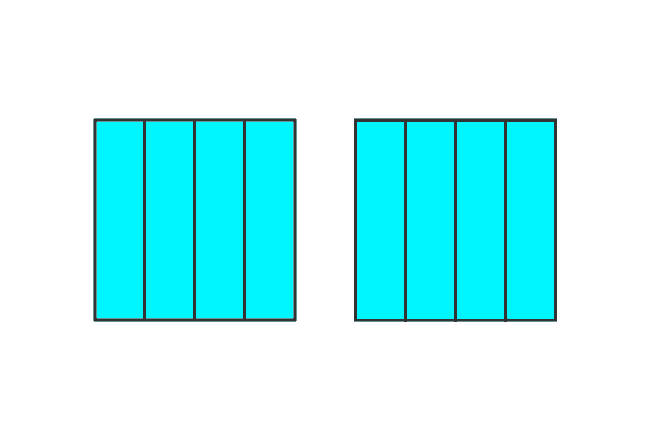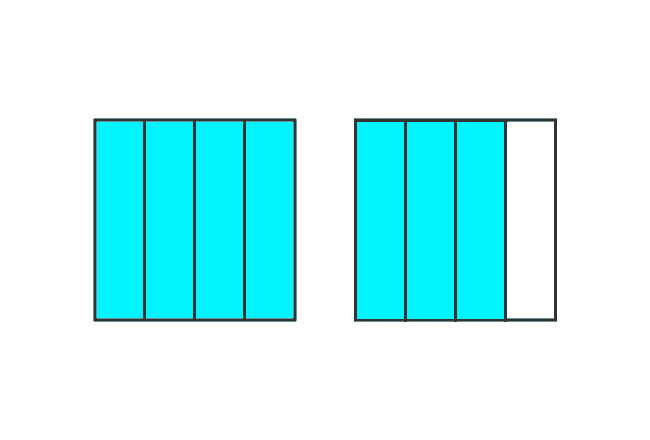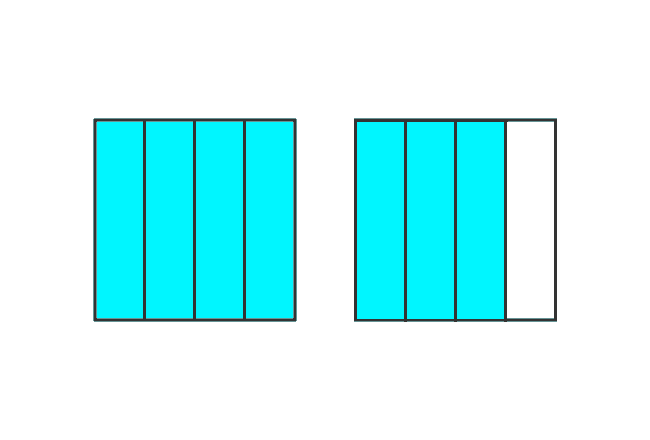
Consider, all parts from one square and three parts from second square.
Fraction = $\dfrac{4}{4} + \dfrac{3}{4}$ = $\dfrac{7}{4}$
It’s expressed as $7 : 4$ in ratio form mathematically. In this example, the value in the numerator is greater than its denominator ($7 > 4$). Hence, it’s known as an improper fraction.
Improper fraction = $\dfrac{7}{4}$
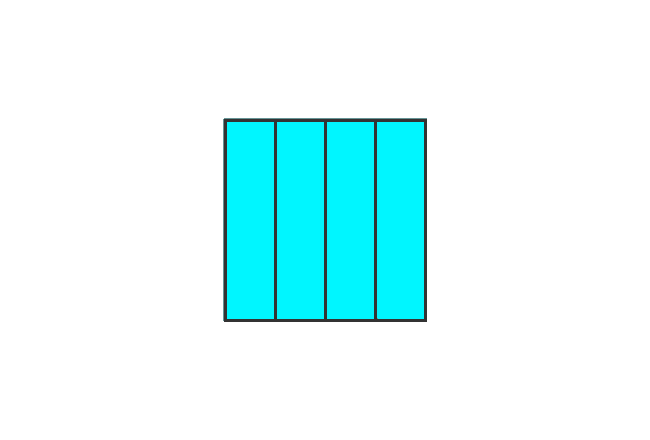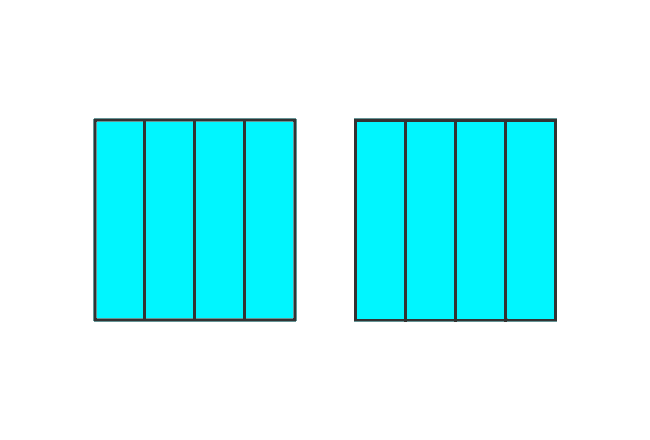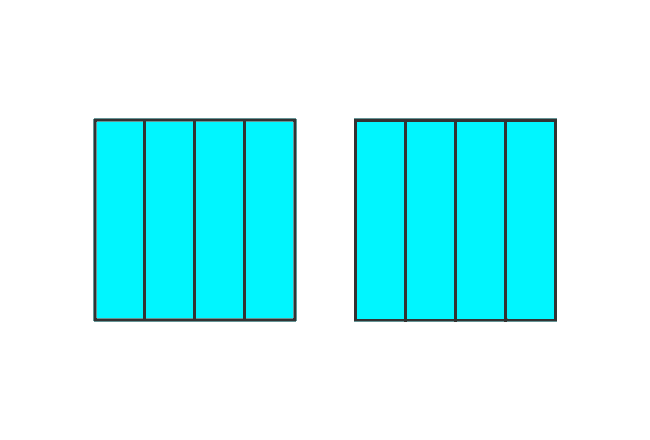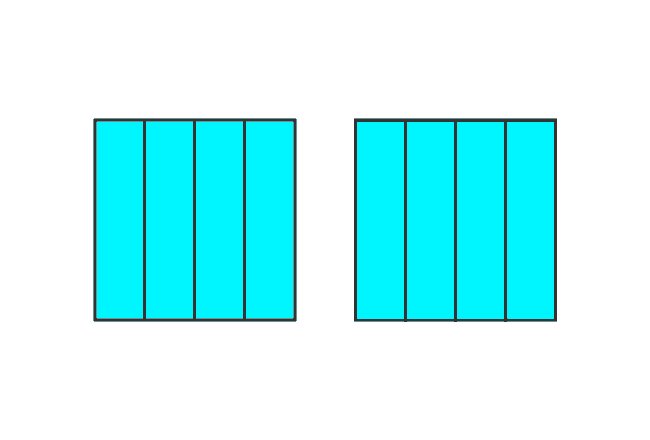
Now, take all parts from two whole quantities.
Fraction = $\dfrac{4}{4} + \dfrac{4}{4}$ = $\dfrac{8}{4}$
It can be written in ratio form as $8 : 4$ in mathematics. The value in the numerator is greater than its denominator ($8 > 4$) and the fraction is known as an improper fraction.
Improper fraction = $\dfrac{8}{4}$
Mathematically, the quantity of this fraction is $2$, which is a whole number but it’s considered as a fraction whenever a whole quantity is written in the form a rational number.
Therefore, the quantities $\dfrac{4}{4}$, $\dfrac{5}{4}$, $\dfrac{6}{4}$, $\dfrac{7}{4}$ and $\dfrac{8}{4}$ are improperly called as fractions and they’re also called as improper fractions due to either same or greater value in the numerator when it’s compared with the value in the denominator.
It’s cleared that the value in the numerator is always greater than or equal to its denominator in the case of an improper fraction. Similarly, any whole number which is expressed in as a rational number, is considered as an improper fraction as well.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved