Ratio

A mathematical approach of comparing two quantities of same kind is called a ratio.

Introduction

Comparison is a method and it is used to know the relation between two quantities but the quantities should be same kind and they should also have the same unit. It is mainly used to know how many times a quantity to another and vice-versa.

The relation between them can be expressed in mathematics in the form of a ratio. A ratio of two quantities is calculated by dividing one quantity by another quantity of same kind.

Example

A boy and his height is $120$ centimetres. A teenager and his height is $180$ centimetres.

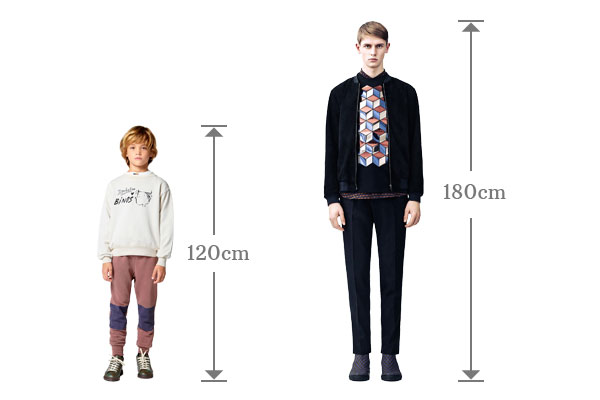
The heights of them can be compared to know how many times the boy is to teenager and also to understand how many times the teenager is to the boy.

Firstly, calculate the ratio of heights of boy to teenager.

$\dfrac{Height \, of \, Boy}{Height \, of \, Teenager} \,=\, \dfrac{120}{180}$

$\implies$ $\dfrac{Height \, of \, Boy}{Height \, of \, Teenager}$ $\,=\,$ $\require{cancel} \dfrac{\cancel{120}}{\cancel{180}}$

$\,\,\, \therefore \,\,\,\,\,\,$ $\dfrac{Height \, of \, Boy}{Height \, of \, Teenager} \,=\, \dfrac{2}{3}$

Representation

The colon $(:)$ punctuation mark is used to represent the ratio of two quantities. The symbol is read as to or is to while pronouncing. The ratio of the quantities is written in mathematics as follows.

$Height \, of \, Boy \,:\, Height \, of \, Teenager \,=\, 2 \,:\, 3$

It is read in two ways mathematically.

1. The ratio of height of boy is to height of teenager is equal to $2$ is to $3$.
2. The ratio of height of boy to height of teenager is equal to $2$ to $3$.

Due to the comparison of the quantities of same kind, a ratio does not have any unit of measurement.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.