Basic Trigonometric formulas

A basic mathematical relation between any trigonometric functions is called a basic trigonometric identity. A basic trigonometric identity is usually used as a formula in mathematics. Hence, it is also called as a basic trigonometric formula.

Basic identities

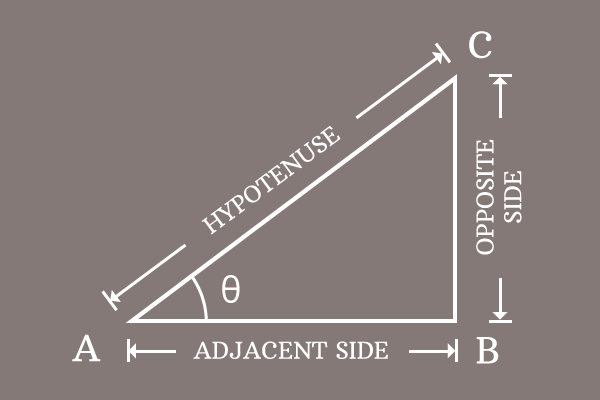
There are four types of basic trigonometric identities in trigonometry and they are used as formulas in mathematics. So, everyone who studies the trigonometry newly must firstly learn all of these basic trigonometric identities.

The following trigonometric formulas derived by taking theta ($\theta$) as angle of a right angled triangle.

Reciprocal identities

Trigonometric ratios form six identities in reciprocal form and learn proofs of these reciprocal formulas.

$(1)\,\,\,\,$ $\sin \theta \,=\, \dfrac{1}{\csc \theta}$

$(2)\,\,\,\,$ $\cos \theta \,=\, \dfrac{1}{\sec \theta}$

$(3)\,\,\,\,$ $\tan \theta \,=\, \dfrac{1}{\cot \theta}$

$(4)\,\,\,\,$ $\cot \theta \,=\, \dfrac{1}{\tan \theta}$

$(5)\,\,\,\,$ $\sec \theta \,=\, \dfrac{1}{\cos \theta}$

$(6)\,\,\,\,$ $\csc \theta \,=\, \dfrac{1}{\sin \theta}$

Product identities

Trigonometric functions form three formulas in product form and learn the proofs of product identities.

$(1)\,\,\,\,$ $\sin \theta \times \csc \theta = 1 $

$(2)\,\,\,\,$ $\cos \theta \times \sec \theta = 1 $

$(3)\,\,\,\,$ $\tan \theta \times \cot \theta = 1 $

Quotient identities

The six trigonometric functions involve in two relations in quotient form and learn the proofs of quotient identities.

$(1)\,\,\,\,$ $\dfrac{\sin \theta}{\cos \theta} = \tan \theta$

$(2)\,\,\,\,$ $\dfrac{\cos \theta}{\sin \theta} = \cot \theta$

Pythagorean identities

The six trigonometric functions form three Pythagorean identities on the basis of Pythagoras Theorem.

$(1)\,\,\,\,$ $\sin^2{\theta} \,+\, \cos^2{\theta} \,=\, 1$

$(2)\,\,\,\,$ $\sec^2{\theta} \,-\, \tan^2{\theta} \,=\, 1$

$(3)\,\,\,\,$ $\csc^2{\theta} \,-\, \cot^2{\theta} \,=\, 1$

Problems

List of the questions for practice to learn how to use the basic trigonometric identities in problems.

Copyright © 2012 - 2022 Math Doubts, All Rights Reserved