What is a Trigonometric ratio?
Fact-checked:
Definition
The ratio between sides of a right triangle is called a trigonometric ratio.
Introduction
In a right triangle, there are three sides and each side has some length naturally. The length of a side can be compared with the length of another side to exactly know how many times a side is to another side of a right-angled triangle. The comparison between any two sides is calculated mathematically by the concept of ratio.
The two different concepts triangle and ratio are combined to compare the sides of a triangle in trigonometry. So, the ratio between any two sides of a right-angled triangle is called the trigonometric ratio.
Now, let’s clearly learn what a trigonometric ratio really is in trigonometry from a visual example.
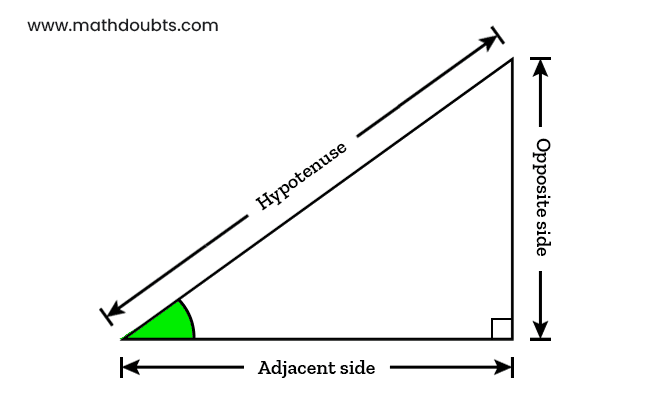
In a right-angled triangle, the names of three edges are opposite side, adjacent side and hypotenuse, and every side has measurable length. Now, the ratio between any two sides can be calculated mathematically by division and their quotient is called a trigonometric ratio.
For example, let’s calculate the ratio of opposite side’s length to the length of adjacent side. It is calculated mathematically by division as follows.
Example
$Trigonometric \, Ratio$ $\,=\,$ $\dfrac{Opposite \, side}{Adjacent \, side}$
Likewise, there are five more ratios in trigonometry and let’s know each trigonometric ratio one after one.
List of Trigonometric Ratios
In trigonometry, there are six ways to calculate the ratio between every two sides with three sides of a right triangle. So, the following are the six ratios between edges of a right-angled triangle in mathematical form.
$\dfrac{Opposite \, side}{Hypotenuse}$
$\dfrac{Adjacent \, side}{Hypotenuse}$
$\dfrac{Opposite \, side}{Adjacent \, side}$
$\dfrac{Adjacent \, side}{Opposite \, side}$
$\dfrac{Hypotenuse}{Adjacent \, side}$
$\dfrac{Hypotenuse}{Opposite \, side}$
Each ratio between every two sides of a right-angled triangle is called a trigonometric ratio, whereas, expressing each ratio as a trigonometric ratio creates confusion in us while discussing about a particular trigonometric ratio. So, a special name for each trigonometric ratio is essential to exactly know whichever trigonometric ratio we talk about.
Names of Trigonometric Ratios
The following are the six special names for six trigonometric ratios.
$Sine$ $\,=\,$ $\dfrac{Opposite \, side}{Hypotenuse}$
$Cosine$ $\,=\,$ $\dfrac{Adjacent \, side}{Hypotenuse}$
$Tangent$ $\,=\,$ $\dfrac{Opposite \, side}{Adjacent \, side}$
$Cotangent$ $\,=\,$ $\dfrac{Adjacent \, side}{Opposite \, side}$
$Secant$ $\,=\,$ $\dfrac{Hypotenuse}{Adjacent \, side}$
$Cosecant$ $\,=\,$ $\dfrac{Hypotenuse}{Opposite \, side}$
Now, remember the trigonometric ratios by their names and let’s start learning the trigonometry further.

