A term that represents a ratio of lengths of adjacent side to hypotenuse at an angle of a right triangle is called the cosine.
Cosine is a name and it actually represents the ratio of lengths of adjacent side to hypotenuse at a particular angle in a right triangle. It can be written in ratio form and also as cosine with angle alternatively.
The value of cosine at an angle is calculated by the ratio of lengths of adjacent side to hypotenuse.
$\dfrac{Length \, of \, Adjacent \, side}{Length \, of \, Hypotenuse}$
Hence, cosine is called as a trigonometric ratio in general.
Alternatively, the value of cosine at an angle is written mathematically by writing cosine in its short form $\cos$ and then respective angle of the right angled triangle.
For example, if angle of right triangle is represented by $x$, then cosine of angle $x$ is written as $\cos{x}$ in trigonometry. $\cos{x}$ is a function form. Therefore, it is usually called as cos function in mathematics.
Thus, cos functions like $\cos{A}$, $\cos{\alpha}$, $\cos{\beta}$, and etc. are defined in mathematics.
$\Delta CAB$ is a right triangle and its angle is denoted by theta ($\theta$).
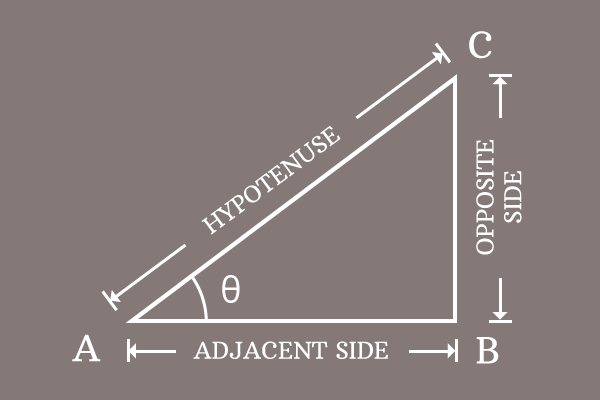
cosine of angle is written as $\cos{\theta}$ in this case.
$\cos{\theta} \,=\, \dfrac{Length \, of \, Adjacent \, side}{Length \, of \, Hypotenuse}$
It can be used as a formula to calculate the value of cosine at any angle of the right triangle.
In this example, $AB$ is length of adjacent side (base) and $AC$ is length of hypotenuse.
$\,\,\, \therefore \,\,\,\,\,\, \cos{\theta} \,=\, \dfrac{AB}{AC}$
The list of exact values of cosine functions in fraction and decimal forms in a table with proofs.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2023 Math Doubts, All Rights Reserved