$\tan{2x}$, $\tan{2\theta}$, $\tan{2A}$ and $\tan{2\alpha}$ are most popular examples for tan double angle function. It is used to expand tan double angle function in terms of tan of angle.
$(1) \,\,\,\,\,\,$ $\tan{2\theta} \,=\, \dfrac{2\tan{\theta}}{1-2\tan^2{\theta}}$
$(2) \,\,\,\,\,\,$ $\tan{2x} \,=\, \dfrac{2\tan{x}}{1-2\tan^2{x}}$
$(3) \,\,\,\,\,\,$ $\tan{2A} \,=\, \dfrac{2\tan{A}}{1-2\tan^2{A}}$
$(4) \,\,\,\,\,\,$ $\tan{2\alpha} \,=\, \dfrac{2\tan{\alpha}}{1-2\tan^2{\alpha}}$
Tan double angle identity in mathematical form is derived in trigonometry by geometrical system.
$\Delta ECD$ is a right angled triangle. Bisect the angle by drawing a line to side $\overline{ED}$ from point $C$ and it intersect the side $\overline{ED}$ at point $F$. Assume, each angle is denoted by theta symbol.
Draw a perpendicular line to side $\overline{CF}$ from point $F$ and it intersects the side $\overline{CE}$ at point $G$. Now, draw a perpendicular line to side $\overline{CD}$ from point $G$. It intersects the side $\overline{CF}$ at point $H$ and also intersects the side $\overline{CD}$ at point $D$.
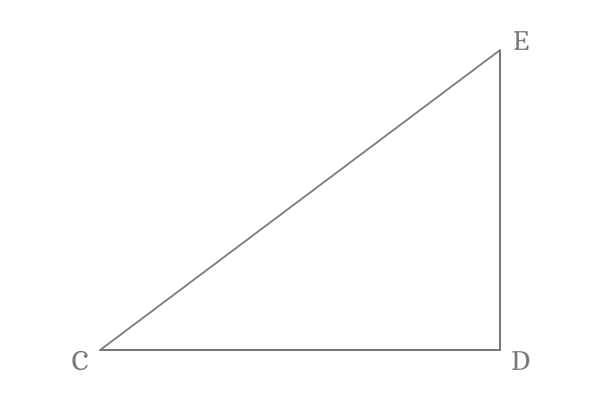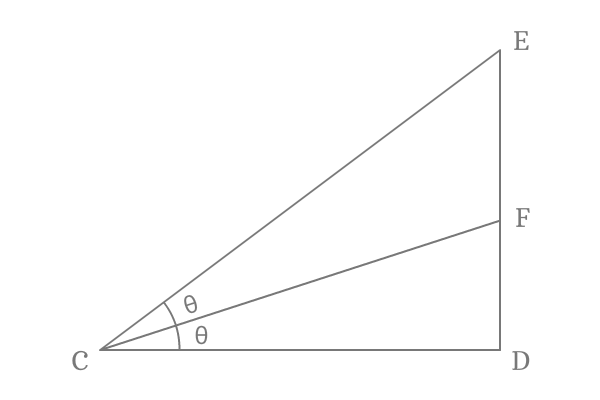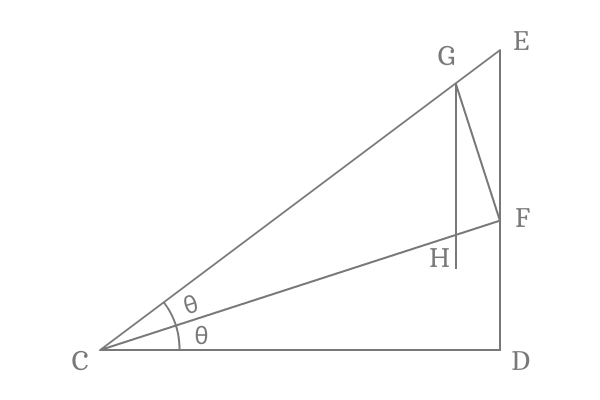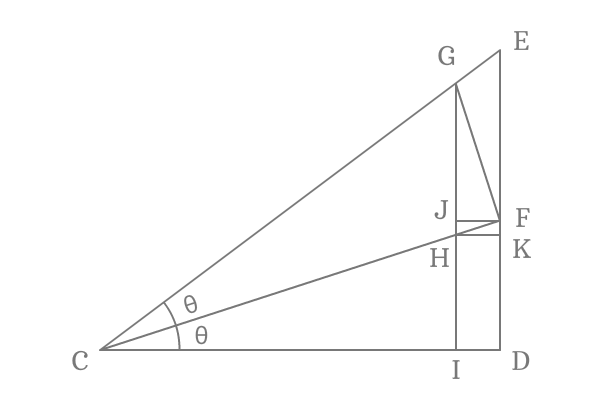
Draw a perpendicular line to side $\overline{GI}$ from point $F$ and it intersects the side $\overline{GI}$ at point $J$. Similarly, draw a perpendicular line to side $\overline{DE}$ from point $H$ and it intersects the side $\overline{ED}$ at point $K$.
$2\theta$ is double angle of $\Delta ICG$. Now, write tan of double angle ($\tan{2\theta}$) in terms of ratio of sides of this triangle.
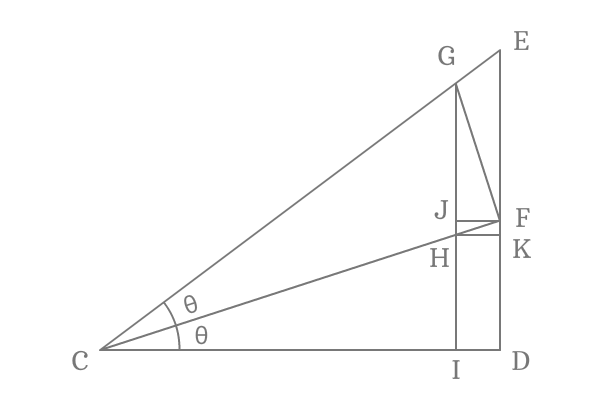
$\tan{2\theta} \,=\, \dfrac{IG}{IC}$
The length of the side $\overline{IG}$ can be written as the sum of the lengths of the sides $\overline{IJ}$ and $\overline{JG}$. Similarly, the length of the side $\overline{IC}$ as the subtraction of length of side $\overline{CD}$ from length of the side $\overline{ID}$.
In other words, $IC = CD–ID$ and $IG = IJ+JG$
$\implies$ $\tan{2\theta} \,=\, \dfrac{IJ+JG}{CD-ID}$
At point $H$, the side $\overline{GI}$ is split into two sides $\overline{GH}$ and $\overline{HI}$. Therefore, the length of the side $\overline{GI}$ can be written as the sum of the lengths of the sides $\overline{GH}$ and $\overline{HI}$.
$\implies \tan{2\theta} \,=\, \dfrac{GH+HI}{CI}$
At point $I$, the side $\overline{CD}$ is divided into two sides $\overline{CI}$ and $\overline{ID}$. So, the length of the side $\overline{CI}$ can be written as the subtraction of the length of the side $\overline{ID}$ from the length of the side $\overline{CD}$.
$\implies \tan{2\theta} \,=\, \dfrac{GH+HI}{CD-ID}$
The sides $\overline{HI}$ and $\overline{FD}$ are parallel lines and the lengths of them are also equal. Due to this reason, the length of the side $\overline{HI}$ can be replaced by the length of the side $\overline{FD}$. Likewise, the sides $\overline{ID}$ and $\overline{HF}$ are parallel lines and their lengths are also equal. So, replace the length of the side $\overline{ID}$ by the length of the side $\overline{HF}$.
$\implies \tan{2\theta} \,=\, \dfrac{GH+FD}{CD-HF}$
Take the length of the $CD$ common from the denominator.
$\implies \tan{2\theta} \,=\, \dfrac{GH+FD}{CD \Bigg(1-\dfrac{HF}{CD}\Bigg)}$
$\implies \tan{2\theta} \,=\, \dfrac{\dfrac{GH+FD}{CD}}{1-\dfrac{HF}{CD}}$
$\implies \tan{2\theta} \,=\, \dfrac{\dfrac{GH}{CD}+\dfrac{FD}{CD}}{1-\dfrac{HF}{CD}}$
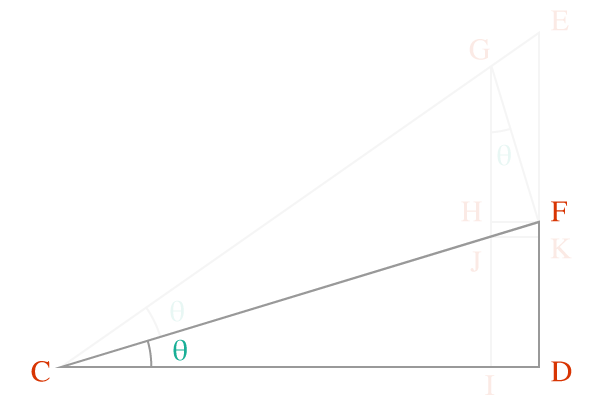
$\overline{FD}$ and $\overline{CD}$ are the sides of the right angled triangle $DCF$. So, consider this triangle and express the ratio of length of the side $\overline{FD}$ to length of the side $\overline{CD}$.
$\tan{\theta} \,=\, \dfrac{FD}{CD}$
Replace the ratio of the sides by the tan function.
$\implies \tan{2\theta} \,=\, \dfrac{\dfrac{GH}{CD}+\tan{\theta}}{1-\dfrac{HF}{CD}}$
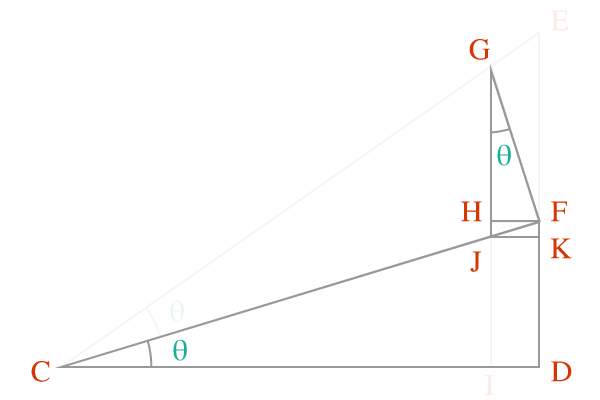
$\overline{GH}$ is the adjacent side of the triangle $HGF$ and $\overline{CD}$ is adjacent side of the $\Delta DCF$. Geometrically, $\Delta HGF$ and $\Delta DCF$ are similar triangles.
Express the lengths of adjacent sides $\overline{GH}$ and $\overline{CD}$ in alternative form.
According to $\Delta HGF$.
$\cos{\theta} \,=\, \dfrac{GH}{FG}$
According to $\Delta DCF$.
$\cos{\theta} \,=\, \dfrac{CD}{CF}$
The two ratios are same. So, make them equal.
$\dfrac{GH}{FG} \,=\, \dfrac{CD}{CF}$
$\implies \dfrac{GH}{CD} \,=\, \dfrac{GF}{CF}$
Replace the ratio of length of the side $\overline{GH}$ to length of the side $\overline{CD}$ by the ratio of length of the side $\overline{CD}$ to length of the side $\overline{CF}$ in the expansion of the cos of double angle formula.
$\implies \tan{2\theta} \,=\, \dfrac{\dfrac{GF}{CF}+\tan{\theta}}{1-\dfrac{HF}{CD}}$
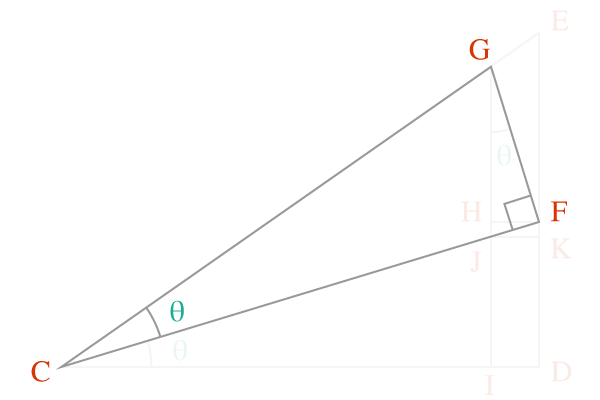
$\overline{GF}$ and $\overline{CF}$ are two sides of the right angled triangle $FCG$.
The ratio of length of the side $\overline{GF}$ to length of the side $\overline{CF}$ is tan of angle theta.
$\tan{\theta} \,=\, \dfrac{GF}{CF}$
Substitute the ratio of length of the side GF to length of the side CF by its equal value.
$\implies \tan{2\theta} \,=\, \dfrac{\tan{\theta}+\tan{\theta}}{1-\dfrac{HF}{CD}}$
$\implies \tan{2\theta} \,=\, \dfrac{2\tan{\theta}}{1-\dfrac{HF}{CD}}$
Once again, use the property of similar triangles of $\Delta HGF$ and $\Delta DCF$.

According to $\Delta HGF$.
$\sin{\theta} \,=\, \dfrac{HF}{GF}$
According to $\Delta DCF$.
$\sin{\theta} \,=\, \dfrac{DF}{CF}$
The two expressions are same. Therefore, make them equal.
$\dfrac{HF}{GF} \,=\, \dfrac{DF}{CF}$
$\implies HF \,=\, \dfrac{DF \times GF}{CF}$
Replace the length of the side $\overline{HF}$ by its equivalent value in the expansion of the tan of double angle law.
$\implies \tan{2\theta} \,=\, \dfrac{2\tan{\theta}}{1-\dfrac{\dfrac{DF \times GF}{CF}}{CD}}$
$\implies \tan{2\theta} \,=\, \dfrac{2\tan{\theta}}{1-\dfrac{DF \times GF}{CD \times CF}}$
$\implies \tan{2\theta} \,=\, \dfrac{2\tan{\theta}}{1-\dfrac{DF}{CD} \times \dfrac{GF}{CF}}$

$\overline{DF}$ and $\overline{CD}$ are the sides of the right angled triangle $DCF$.
Express the ratio of the length of the side $\overline{DF}$ to length of the side $\overline{CD}$ and it is the equal to tan of the angle theta.
$\tan{\theta} \,=\, \dfrac{DF}{CD}$
Replace the value of the ratio of the sides in the formula.
$\implies \tan{2\theta} \,=\, \dfrac{2\tan{\theta}}{1-\tan{\theta} \times \dfrac{GF}{CF}}$

$\overline{GF}$ and $\overline{CF}$ are two sides of the right angled triangle $FCG$. So, the ratio of length of the side $\overline{GF}$ to length of the side $\overline{CF}$ in trigonometric function form.
$\tan{\theta} \,=\, \dfrac{GF}{CF}$
Write the ratio of the sides as the tan of angle theta to complete the proof of tan of double angle rule geometrically.
$\implies \tan{2\theta} \,=\, \dfrac{2\tan{\theta}}{1-\tan{\theta} \times \tan{\theta}}$
$\therefore \,\,\,\,\,\, \tan{2\theta} \,=\, \dfrac{2\tan{\theta}}{1-\tan^2{\theta}}$
The trigonometric formula is mainly used to expand the tan of double angle in terms of tan of angle and can also use in reverse operation.
Take $\theta \,=\, 30^\circ$ and check both sides of the formula.
$\tan{(2 \times 30^\circ)}$
$=\,\,\, \tan{(60^\circ)}$
$=\,\,\, \sqrt{3}$
Now, evaluate the expansion of the tan of the double angle.
$\dfrac{2\tan{(30^\circ})}{1-\tan^2{(30^\circ)}}$
$=\,\,\, \dfrac{2 \times \dfrac{1}{\sqrt{3}}}{1-{\Bigg(\dfrac{1}{\sqrt{3}}\Bigg)}^2}$
$=\,\,\, \dfrac{\dfrac{2}{\sqrt{3}}}{1-\dfrac{1}{3}}$
$=\,\,\, \dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{3-1}{3}}$
$=\,\,\, \dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{2}{3}}$
$=\,\,\, \dfrac{2}{\sqrt{3}} \times \dfrac{3}{2}$
$=\,\,\, \dfrac{2 \times 3}{\sqrt{3} \times 2}$
$\require{cancel} =\,\,\, \dfrac{\cancel{2} \times 3}{\sqrt{3} \times \cancel{2}}$
$=\,\,\, \dfrac{3}{\sqrt{3}}$
$=\,\,\, \sqrt{3}$
Compare both results and they both are equal. Hence, the tan of double angle formula is called as a double angle trigonometric identity.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved