$\tan{(45^°)}$ Proof

The value of tan of $45$ degrees can be derived mathematically in three ways. One of them is a trigonometric approach and the other two methods are purely geometrical approaches but there is a slight difference between the geometrical methods.

Theoretical approach

The value of $\tan{(45^°)}$ can be derived exactly by theoretical approach of geometry on the basis of a geometric property, which reveals the direct relation between opposite and adjacent sides when angle of right angled triangle is $\dfrac{\pi}{4}$.

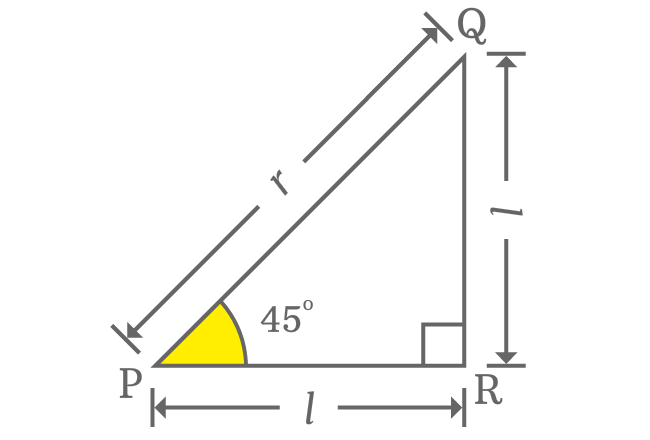
$\tan{(45^°)}$ $\,=\,$ $\dfrac{Length \, of \, Opposite \, side}{Length \, of \, Adjacent \, side}$

$\implies \tan{(45^°)} \,=\, \dfrac{QR}{PR}$

When angle of right triangle is $45$ degrees, the length of opposite side is exactly equal to the length of adjacent side. In this case, the length of both opposite side and adjacent side is denoted by $l$.

$\implies \tan{(45^°)} \,=\, \dfrac{l}{l}$

$\implies \tan{(45^°)} \,=\, \require{cancel} \dfrac{\cancel{l}}{\cancel{l}}$

$\,\,\, \therefore \,\,\,\,\,\, \tan{(45^°)} \,=\, 1$

Practical approach

It is not an issue if you don’t know the geometric property of opposite and adjacent sides when angle of right triangle is $50^g$. You can evaluate the exact value of $\tan{(50^g)}$ on your own by constructing a right triangle with $45$ degrees angle by your geometrical tools.

1. Draw a straight line from a point $J$.
2. After that, coincide the point $J$ with centre of the protractor and also coincide the right side base line of protractor with horizontal line. Now, mark a point at $45$ degrees angle.
3. Draw a straight line by a ruler by Joining point $J$ and a point, marked at $45$ degrees angle.
4. Now, set some distance between needle and pencil points of compass. In this example, $12 \, cm$ is set. Then, draw an arc on the $45^°$ angle line from point $J$ and it cuts the line at point $K$.
5. Now, draw a perpendicular line to horizontal line from point $K$ by set square and it intersects the horizontal line at point $L$. It forms a right triangle geometrically, known as $\Delta LJK$.

Now, you can start the procedure to find the exact value of tan of angle $45$ degrees from $\Delta LJK$ by expressing it in terms of lengths of the respective sides.

$\tan{(45^°)} = \dfrac{Length \, of \, Opposite \, side}{Length \, of \, Adjacent \, side}$

$\implies \tan{(45^°)} \,=\, \dfrac{KL}{JL}$

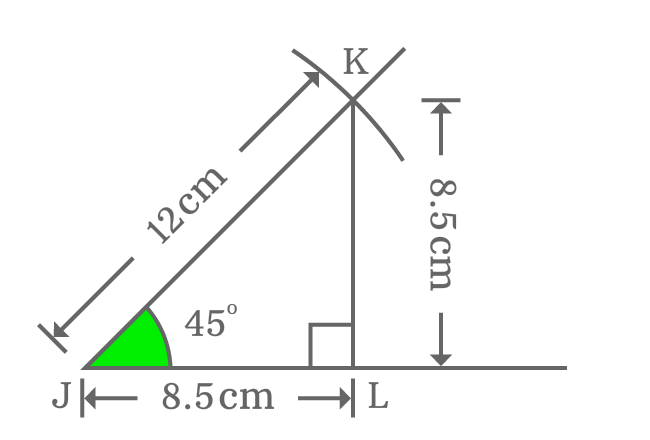
In this example, the lengths of opposite and adjacent sides are unknown. So, measure the lengths of both opposite side ($KL$) and adjacent side ($JL$) by ruler.

You will observe that the lengths of both opposite side and adjacent side are equal and length of each of them is nearly $8.5$ centimetres.

$\implies \tan{(45^°)} \,=\, \dfrac{KL}{JL} = \dfrac{8.5}{8.5}$

$\implies \tan{(45^°)} \,=\, \require{cancel} \dfrac{\cancel{8.5}}{\cancel{8.5}}$

$\,\,\, \therefore \,\,\,\,\,\, \tan{(45^°)} \,=\, 1$

Trigonometric approach

The value of $\tan{\Big(\dfrac{\pi}{4}\Big)}$ can be evaluated exactly by the ratio or quotient identity of sin and cos functions. It is actually evaluated by the ratio of of sin $45$ degrees value to cos $45$ degrees value.

$\tan{(45^°)} \,=\, \dfrac{\sin{(45^°)}}{\cos{(45^°)}}$

$\implies \tan{(45^°)} \,=\, \dfrac{\dfrac{1}{\sqrt{2}}}{\dfrac{1}{\sqrt{2}}}$

$\implies \tan{(45^°)} \,=\, \dfrac{1}{\sqrt{2}} \times \dfrac{\sqrt{2}}{1}$

$\implies \tan{(45^°)} \,=\, \dfrac{1 \times \sqrt{2}}{\sqrt{2} \times 1}$

$\implies \tan{(45^°)} \,=\, \dfrac{\sqrt{2}}{\sqrt{2}}$

$\implies \tan{(45^°)} \,=\, \require{cancel} \dfrac{\cancel{\sqrt{2}}}{\cancel{\sqrt{2}}}$

$\,\,\, \therefore \,\,\,\,\,\, \tan{(45^°)} \,=\, 1$

Verdict

The three mathematical methods have proved that the exact value of $\tan{\Big(\dfrac{\pi}{4}\Big)}$ is equal to one.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.