Proof of Sine even or odd identity

According to even-odd identity of sine function, the sine of negative angle is equal to negative sign of sine of angle.

$\sin{(-\theta)} \,=\, -\sin{\theta}$

This negative angle trigonometric identity of sine function can be proved geometrically in mathematical form.

Construction of a Right triangle with Positive angle

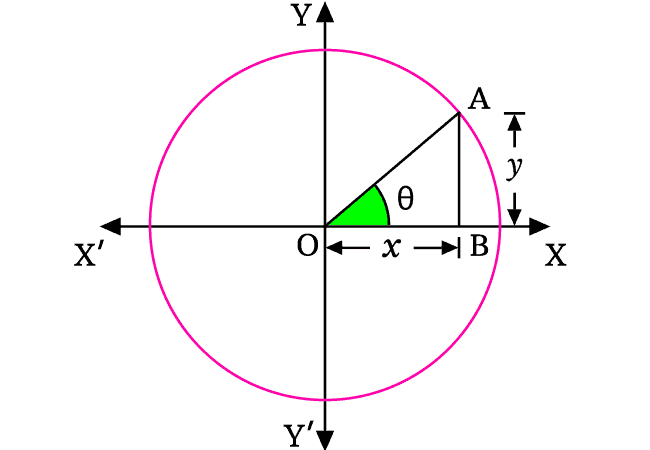
A line segment is rotated in anticlockwise direction from zero angle position to make an angle with horizontal axis. The line segment is mathematically expressed as $\overline{OA}$ at its final position.

The angle made by the line segment $OA$ with horizontal axis is denoted by a symbol theta.

A perpendicular line to positive $x$ axis is drawn from point $A$ and it intersects the axis perpendicularly at point $B$. Thus, a right triangle $AOB$ is constructed geometrically and it is written as $\Delta AOB$ in mathematics.

In the first quadrant, the divisions of both coordinate axes are represented by positive values. Hence, the lengths of adjacent side and opposite side are denoted by $x$ and $y$ algebraically.

According to the $\Delta AOB$, the sine of angle theta can be written mathematically in ratio form.

$\sin{\theta} \,=\, \dfrac{AB}{OA}$

$\implies$ $\sin{\theta} \,=\, \dfrac{y}{OA}$

Actually, the length of hypotenuse is unknown but it can be evaluated from the lengths of opposite and adjacent sides by the Pythagorean Theorem.

$OA$ $\,=\,$ $\sqrt{OB^2+AB^2}$ $\,=\,$ $\sqrt{x^2+y^2}$

$\implies$ $\sin{\theta} \,=\, \dfrac{y}{\sqrt{x^2+y^2}}$

Construction of Right triangle with Negative angle

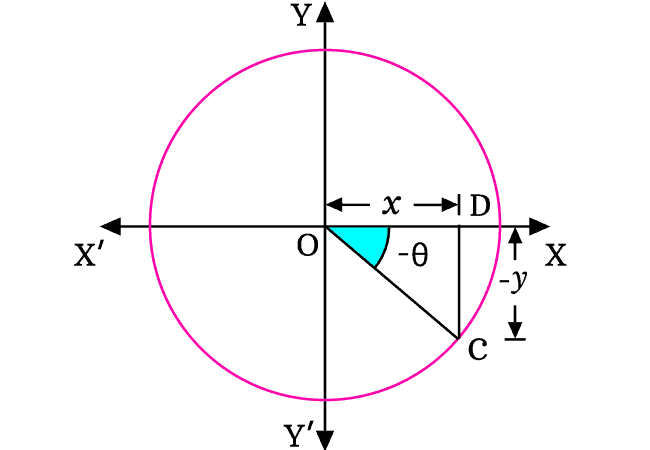
A line segment is rotated in clockwise direction from zero angle position to make same angle with horizontal axis. The line segment is written mathematically as $\overline{OC}$ at its final position.

The angle made by the line segment $OC$ with horizontal axis is denoted by same symbol theta but the line is rotated in clockwise direction. Hence, the angle is written as negative theta ($-\theta$) as per sense of angle system.

From point $C$, a perpendicular line is drawn to horizontal axis and it intersects the $x$ axis perpendicularly at point $D$. In this way, a right angled triangle (expressed as $\Delta COD$) is constructed geometrically.

In the fourth quadrant, each division of $x$ axis is denoted by a positive value but each division of $y$ axis is denoted by a negative value. Therefore, the lengths of adjacent side and opposite side are represented in algebraic form as $x$ and $-y$ respectively.

According to the $\Delta COD$, the sine of angle negative theta can be written in ratio form in mathematical form.

$\sin{(-\theta)} \,=\, \dfrac{CD}{OC}$

$\implies$ $\sin{(-\theta)} \,=\, \dfrac{-y}{OC}$

The length of hypotenuse can be evaluated from the lengths of opposite side and adjacent side by the Pythagorean Theorem.

$OA$ $\,=\,$ $\sqrt{OC^2+CD^2}$ $\,=\,$ $\sqrt{x^2+(-y)^2}$

$\implies$ $OA$ $\,=\,$ $\sqrt{OC^2+CD^2}$ $\,=\,$ $\sqrt{x^2+y^2}$

$\implies$ $\sin{(-\theta)} \,=\, \dfrac{-y}{\sqrt{x^2+y^2}}$

Revealing the Relation between Sine functions

According to the above two steps, the sine functions are expressed in ratio form of the sides of the two triangles.

$\sin{\theta} \,=\, \dfrac{y}{\sqrt{x^2+y^2}}$

$\sin{(-\theta)} \,=\, -\dfrac{y}{\sqrt{x^2+y^2}}$

The value of sine of angle theta is also in the value of the sine of negative angle theta but it is with negative symbol.

$\implies$ $\sin{(-\theta)} \,=\, -(\sin{\theta})$

$\,\,\, \therefore \,\,\,\,\,\,$ $\sin{(-\theta)} \,=\, -\sin{\theta}$

Geometrically, it is proved that the sine of negative angle is equal to the negative sign of sine of angle. It is called as sine of negative angle identity or even-odd identity of sine function in trigonometry mathematics.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.