Proof of $\sin{(30^°)}$ in Practical Geometric method
By Ashok Kumar, B.E. | Fact-checked:
The value of sin of $30$ degrees can be derived in theoretical approach but it requires knowledge on properties of right triangle when its angle is equal to $30^°$. You can even find the value of sin of angle $30$ degrees geometrically by constructing a right triangle with $30$ degrees angle with the help of geometric tools.

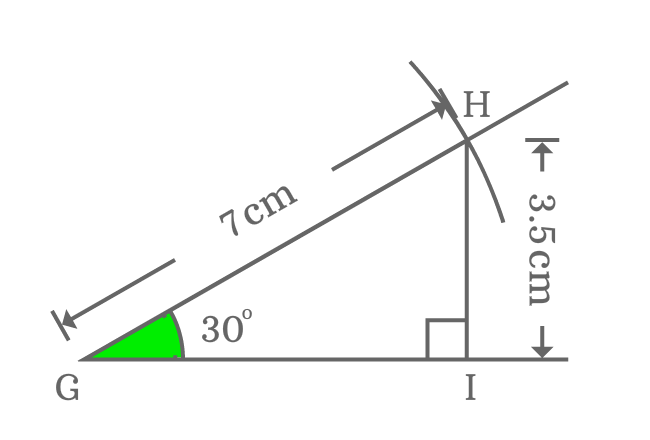
- From point $\small G$, draw a straight line on a plane horizontally.
- Draw a $30$ degrees line from point $\small G$ by using protractor and ruler.
- Set compass to any length. It is set to $7 \, cm$ in this case by considering measurement of ruler. Later, draw an arc on $30$ degrees line from point $\small G$ and it intersects the $30$ degrees line at point $\small H$.
- Finally, draw a perpendicular line to horizontal line from point $\small H$ and it intersects the horizontal line perpendicularly at point $\small I$. This procedure constructs a right triangle (called $\small \Delta IGH$) geometrically.
In $\Delta IGH$, the length of hypotenuse is $GH = 7 \, cm$ and the angle of right triangle is $30$ degrees. So, write sin of angle $30$ degrees in the form of ratio of lengths of the sides.
$\sin{(30^°)} \,=\, \dfrac{HI}{GH}$
The length of opposite side is required to calculate the exact value of sin $30$ degrees. So, take a ruler and measure the length of the opposite side. You will measure that the length of opposite side is $3.5 \, cm$ exactly.
$\implies \sin{(30^°)} \,=\, \dfrac{3.5}{7}$
$\implies \require{cancel} \sin{(30^°)} \,=\, \dfrac{\cancel{3.5}}{\cancel{7}}$
$\implies \sin{(30^°)} \,=\, \dfrac{1}{2}$
It is exact value of sin of $30$ degrees in fraction and its value in decimal is given below.
$\,\,\, \therefore \,\,\,\,\,\, \sin{(30^°)} \,=\, 0.5$
In this way, the value of sine of angle $30$ degrees can be derived experimentally in trigonometry by using geometric tools.

