Proof of $\sin{(15^\circ)}$ in Geometric method

The value of sine of angle fifteen degrees is exactly equal to the square root of six minus square root of two divided by four, or square root of three minus one divided by two times square root of two.

$\sin{(15^\circ)}$ $\,=\,$ $\dfrac{\sqrt{6}-\sqrt{2}}{4}$ $\,=\,$ $\dfrac{\sqrt{3}-1}{2\sqrt{2}}$

Sine of angle $15^\circ$ represents a value, which is calculated by a ratio of length of opposite side to length of hypotenuse in a $15^\circ$ right triangle.

So, it is essential to construct a right angled triangle with an angle of $15^\circ$ for calculating the sine of angle fifteen degrees in geometrical method.

Construct the Triangle with 15 degrees

Let’s learn how to construct a right triangle with an angle of fifteen degrees in geometric system.

1. Draw a line from a point on a plane by a ruler in centimeters. Here, $8$ centimetres line segment is drawn horizontally and its endpoints are denoted by $O$ and $K$.
2. Draw a straight line with an angle of fifteen degrees from point $O$ by coinciding center of a protractor with point $O$ and also coinciding its right side base line with horizontal line.
3. Finally, draw perpendicular line to horizontal line from point $K$ towards $15^\circ$ degrees line for intersecting it at point $L$. Thus, a right triangle is constructed with an angle of fifteen degrees.

Measure the Length of the sides

The lengths of both opposite side and hypotenuse should be known to us in order to calculate the sine in a fifteen degrees right angled triangle.

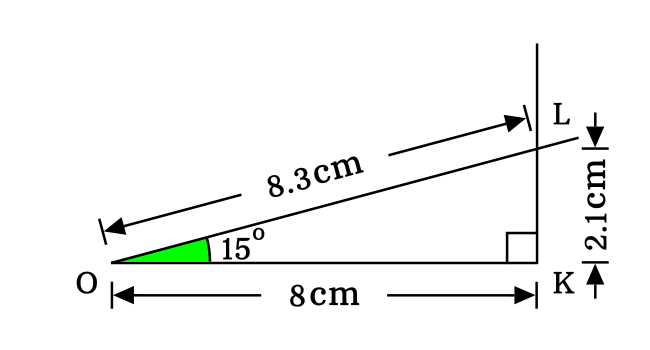
In $\Delta LOK$, the opposite side and hypotenuse are $\overline{LK}$ and $\overline{OL}$ respectively and their corresponding lengths are $LK$ and $OL$.

Now, measure the distance from point $K$ to $L$ for knowing the length of the opposite side by using a ruler in centimeters. Similarly, measure the distance from point $O$ to $L$ in order to know the length of the hypotenuse.

$(1).\,\,\,$ $LK \,=\, 2.1\, cm$

$(2).\,\,\,$ $OL \,=\, 8.3\, cm$

Calculate the Sine of angle 15 degrees

According to the $\Delta LOK$, define the sine of angle fifteen degrees in ratio form for calculating its value.

$\sin{(15^\circ)} \,=\, \dfrac{LK}{OL}$

It measured that the length of the opposite side is $2.1 \, cm$ and the length of hypotenuse is $8.3 \, cm$ in the right triangle.

$\implies$ $\sin{(15^\circ)} \,=\, \dfrac{2.1}{8.3}$

$\implies$ $\sin{(15^\circ)} \,=\, 0.2530120481\cdots$

$\,\,\,\therefore\,\,\,\,\,\,$ $\sin{(15^\circ)} \,\approx\, 0.253$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.