Roster notation

A method of listing the elements in a row with comma separation within curly brackets is called the roster notation.

Introduction

The roster notation is a simple mathematical representation of a set in mathematical form.

In this method, the elements (or members) are enumerated in a row inside the curly brackets. If the set contains more than one element, then every two elements are separated by a comma symbol.

Due to the listing of elements one after one, the roster method is also called the enumeration notation.

Examples

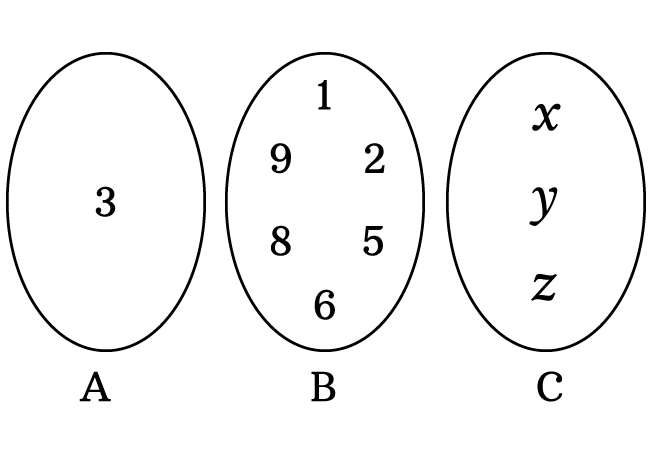
In set $A$, there is only one element. Hence, the element $3$ is displayed within curly brackets.

$A \,=\, \Big\{3\Big\}$

In sets $B$ and $C$, we have more than one member. Hence, the members are listed one after one between curly brackets with comma separation.

$B \,=\, \Big\{1, 2, 5, 6, 8, 9\Big\}$

$C \,=\, \Big\{x, y, z\Big\}$

This mathematical form is called the roster form or enumeration form.

Limitations

The roster method is very simple method for representing a set in mathematical form but it has some limitations.

More elements

The roster notation is not comfortable to express many elements in roster form.

$D \,=\, \Big\{1,$ $2,$ $3,$ $4,$ $5,$ $6,$ $7,$ $8,$ $9,$ $10,$ $11,$ $12,$ $13,$ $14,$ $15,$ $16,$ $17,$ $18,$ $19,$ $20\Big\}$

$E \,=\, \Big\{a,$ $b,$ $c,$ $d,$ $e,$ $f,$ $g,$ $h,$ $i,$ $j,$ $k,$ $l,$ $m,$ $n,$ $o,$ $p,$ $q,$ $r,$ $s,$ $t,$ $u,$ $v,$ $w,$ $x,$ $y,$ $z\Big\}$

The set $D$ expresses the roster form of the numbers from $1$ to $20$. Similarly, the set $E$ expresses the roster form of alphabets from $a$ to $z$.

The two sets are lengthy and it is not convenient for writing such sets in roster form. Just imagine the roster form of a set if the set contains more than $100$ elements. It becomes a nightmare for everyone to write it. However, some sets follow a pattern or have a particular sequence.

In order to overcome this issue, the first three or four members along with a continuous symbol and last element are written between the curly braces.

$D \,=\, \Big\{1, 2, 3, \ldots, 20\Big\}$

$E \,=\, \Big\{a, b, c, d, \ldots, z\Big\}$

Some sets have infinite elements. It is not actually possible to express all of them in roster form. Similarly, we don’t know the last element in these types of sets. If sets follow a pattern or have a particular sequence, we just write the first three or four elements with a continuous symbol within the curly braces.

The set $F$ represents the odd numbers in natural numbers.

$F \,=\, \Big\{1, 3, 5, \ldots \Big\}$

$F \,=\, \Big\{1, 3, 5, 7, \ldots \Big\}$

Repeated elements

The actual problem comes to the roster method with repeated elements in the set. If the elements are few, we can easily express the set in roster form as follows.

$G$ $\,=\,$ $\Big\{0,$ $1,$ $2,$ $3,$ $2,$ $5,$ $0,$ $9$ $\Big\}$

If the set contains many elements with repeated elements, it is either uncomfortable or impossible to express the elements in roster notation because the elements do not follow a pattern or have a particular sequence. In this case only, the roster notation is not recommendable in set theory.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.