
An angle of more than $180^\circ$ but less than $360^\circ$ is called a Reflex angle.
The region from more than $180^\circ$ to less than $360^\circ$ is called reflex. If the angle lies in this region, the angle is known as the reflex angle geometrically.
Geometrically, reflex angles are formed possibly in two different cases.
The angle of a line is usually measured from $0^\circ$ angle. So, assume the ray $\overrightarrow{RS}$ is initially at zero degrees angle.
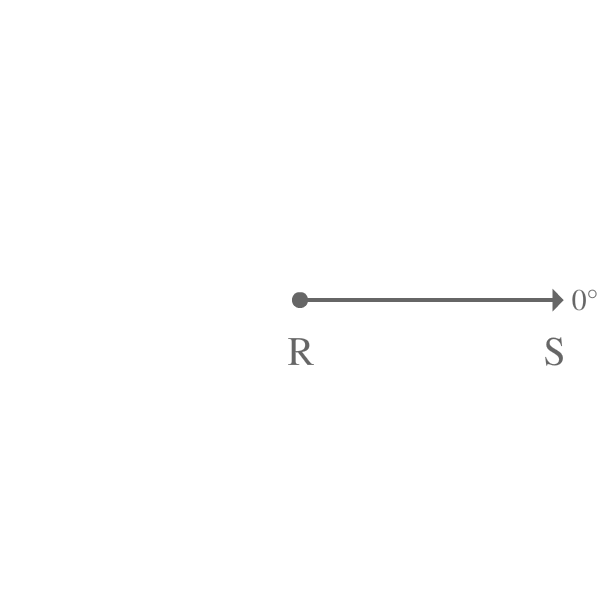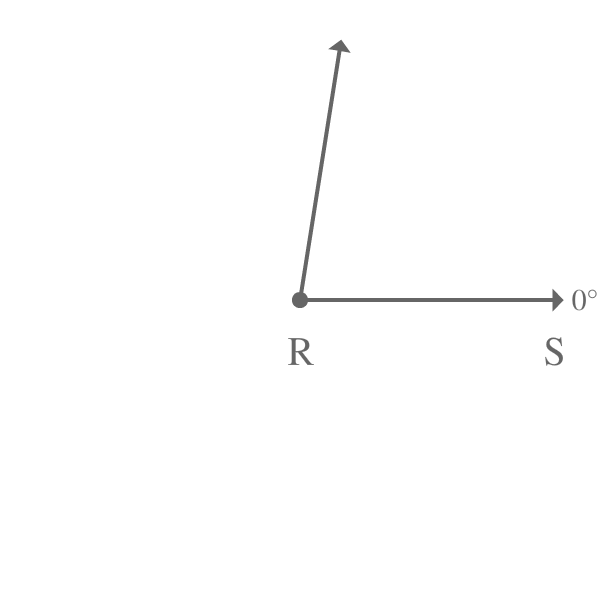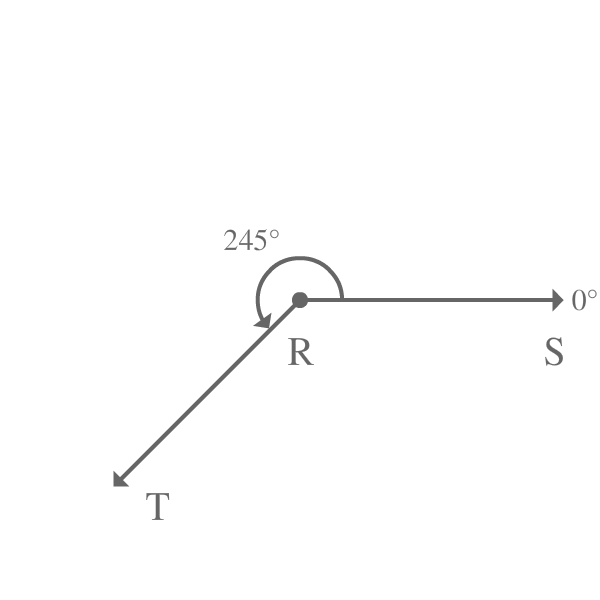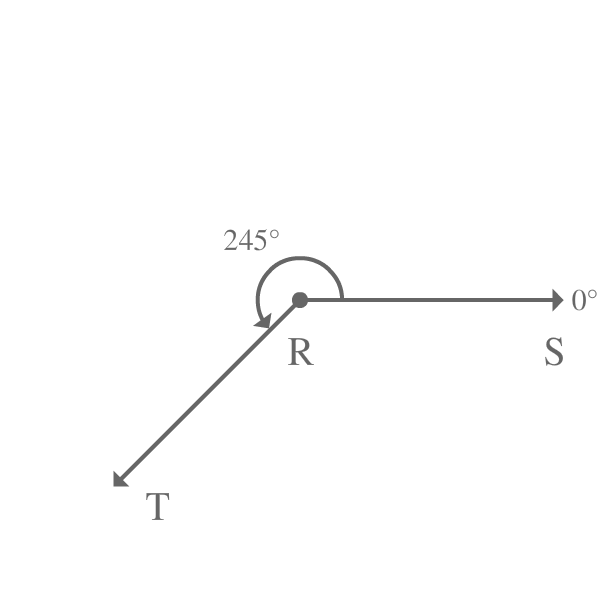
Later, the ray $\overrightarrow{RS}$ is rotated to $245^\circ$ angle in anticlockwise direction to reach new position where the ray $\overrightarrow{RS}$ is called as $\overrightarrow{RT}$.
In other words, the ray $\overrightarrow{RS}$ made an angle of $245^\circ$ to reach its final position from its initial position.
$\angle SRT = 245^\circ$
The angle $SRT$ is $245^\circ$ and it is greater than $180^\circ$ but less than $360^\circ$. Therefore, the $\angle SRT$ is called as a reflex angle.
If any straight line makes an angle of greater than $180^\circ$ and less than $360^\circ$ by the rotation, the angle is called as a reflex angle.

$U$ is a point where two rays $\overrightarrow{UV}$ and $\overrightarrow{UW}$ are started.
In this case, the ray $\overrightarrow{UV}$ becomes reference line to ray $\overrightarrow{UW}$ and vice-versa to measure angle between them.
The angle between them is measured as $310^\circ$ and it is denoted by $\angle VUW$.
$\angle VUW = 310^\circ$
The angle $VUW$ is greater than $180^\circ$ and less than $360^\circ$. Therefore $\angle VUW$ is called as reflex angle.
As example here, if angle between any two lines is greater than 180 and less than 360, the angle between them is an example to the reflex angle.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved