Obtuse angle

Definition

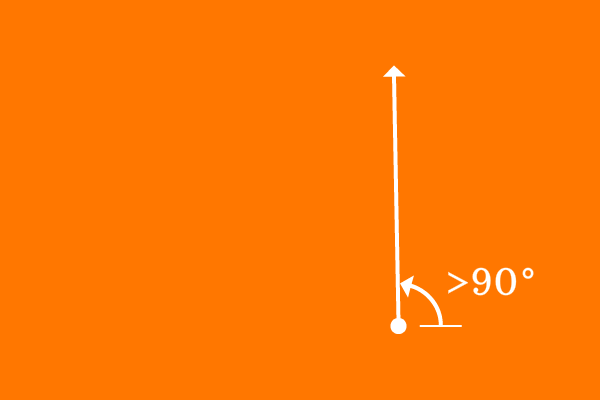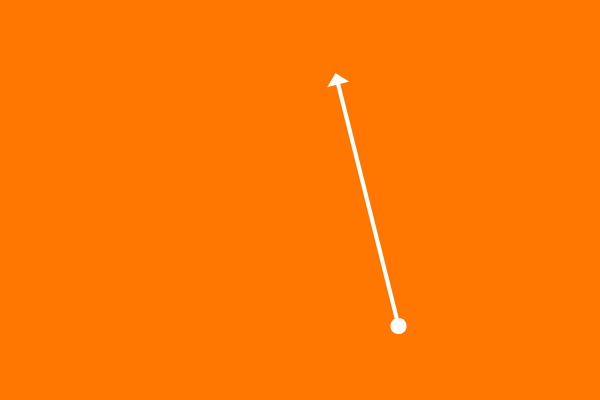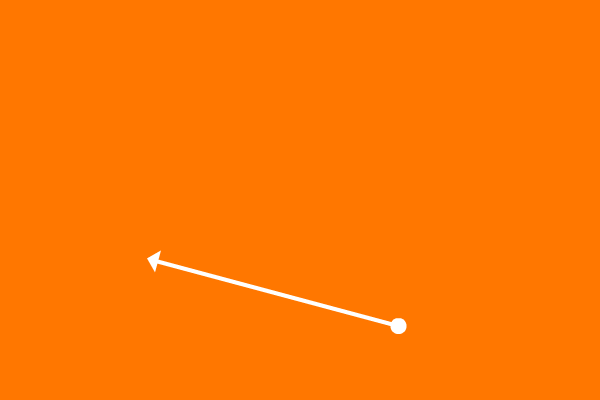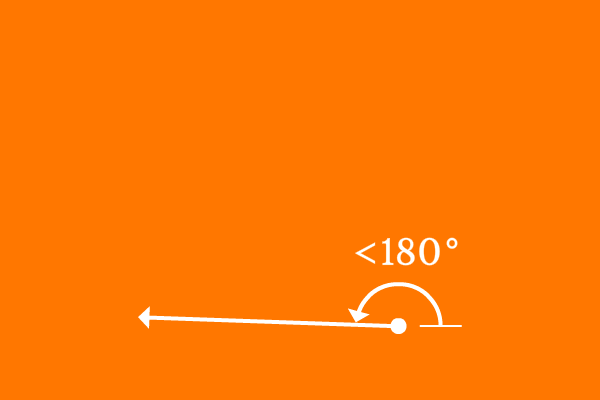
An angle of more than $90^°$ but less than $180^°$ is called an obtuse angle.

The meaning of an obtuse angle is, the angle of greater than $90^\circ$ and less than $180^\circ$. So, an angle which lies between $90^\circ$ and $180^\circ$ is called an obtuse angle.

So, the range of an obtuse angle can be written as $(90^\circ, 180^\circ)$ in mathematics.

Case study

In geometric system, obtuse angles are formed in two possible ways.

The angle of a line is measured from zero degrees line. If a line makes an angle more than $90^\circ$ and less than $180^\circ$ with surface of the earth, the angle is called as an obtuse angle.

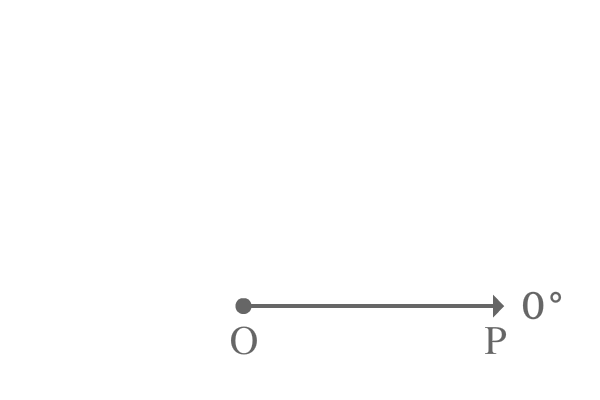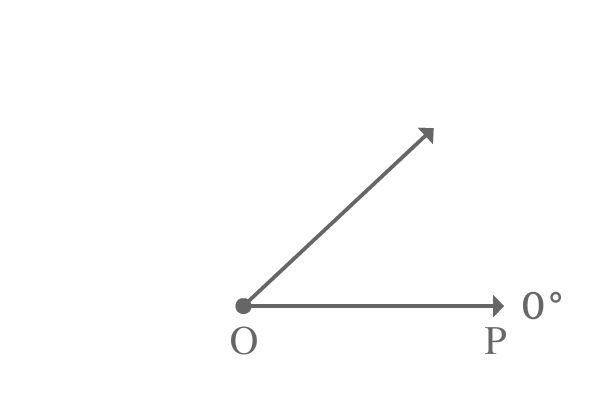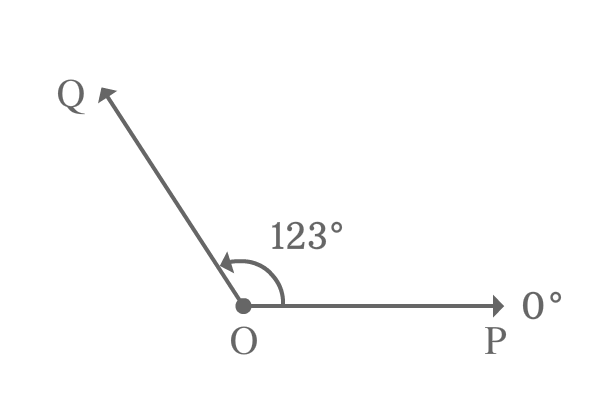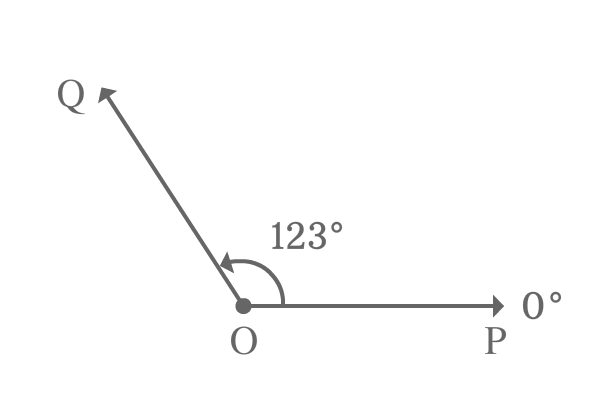
$\overrightarrow{OP}$ is a ray and it is at zero angle at its initial position.

The same ray is rotated an angle of $123^\circ$ in anticlockwise direction to reach its final position where the ray $\overrightarrow{OP}$ is become $\overrightarrow{OQ}$.

The ray is made an angle of $123^\circ$ from its initial position to final position.

$\angle QOP = 123^\circ$

The angle $QOP$ is more than $90^\circ$ but less than $180^\circ$. Hence, the angle made by the ray $\overrightarrow{OP}$ to reach from its initial position to final position is an example to an obtuse angle.

The angle between any two lines which have a common vertex is measured by considering one line as baseline to another and vice-versa to measure the angle. If the angle between them is greater than $90^\circ$ and less than $180^\circ$, the angle is called as an obtuse angle in geometric system.

$\overrightarrow{RS}$ and $\overrightarrow{RT}$ are two rays and they both are started travelling from a point $R$.

The two rays $\overrightarrow{RS}$ and $\overrightarrow{RT}$ continued travelling infinitely from point $R$. The angle between them is measured by taking one line as baseline to another line and vice-versa.

The angle between the rays $\overrightarrow{RS}$ and $\overrightarrow{RT}$ is measured as $165^\circ$ angle.

$\angle SRT = 165^\circ$

The angle $SRT$ is more is greater than $90^\circ$ but less than $180^\circ$. Therefore, the angle between rays $\overrightarrow{RS}$ and $\overrightarrow{RT}$ is an example for an obtuse angle.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.