A system of expressing the number of rows and columns of a matrix in mathematical form is called the order of a matrix.
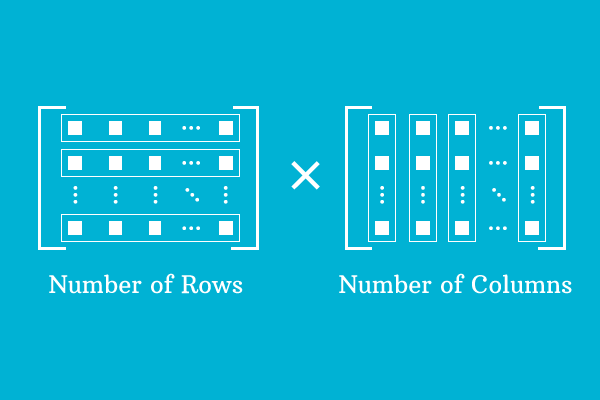
The order of a matrix denotes the arrangement of elements as number of rows and columns in a matrix. So, it is known as dimension of a matrix. It is usually expressed as the number of rows is multiplied by the number of columns in mathematics but it is read as number of rows by number of columns.
One important factor is, the dimension of the matrix tells the number of elements of the matrix. It can be obtained by multiplying the rows by columns.
$M =
\begin{bmatrix}
e_{11} & e_{12} & e_{13} & \cdots & e_{1n} \\
e_{21} & e_{22} & e_{23} & \cdots & e_{2n} \\
e_{31} & e_{32} & e_{33} & \cdots & e_{3n} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
e_{m1} & e_{m2} & e_{m3} & \cdots & e_{mn}
\end{bmatrix}
$
In general form matrix, the elements are arranged as $m$ rows and $n$ columns. So, the order of the matrix is $m \times n$ and it is read as $m$ by $n$.
The order of a matrix is useful to find the number of elements in any type of matrix. For example, the total number of elements in matrix $M = m \times n = mn$
$A =
\begin{bmatrix}
-7
\end{bmatrix}
$
There is only one row and column in matrix $A$. The matrix $A$ is called a matrix of order $1 \times 1$ and read as one by one matrix. Simply, it is called as a matrix of order $1$.
The total number of elements in matrix $A = 1 \times 1 = 1$
$B =
\begin{bmatrix}
1 & 5 & 3
\end{bmatrix}
$
There is one row and three columns in matrix $B$. So, it is called a matrix of order $1 \times 3$ and read as one by three matrix.
The total number of elements in matrix $B = 1 \times 3 = 3$
$C =
\begin{bmatrix}
6 & -2 \\
0 & 3
\end{bmatrix}
$
The elements are arranged in matrix $C$ in $2$ rows and $2$ columns. It is called a matrix of order $2 \times 2$ and read as two by two matrix but simply a matrix of order $2$.
The total number of elements in matrix $C = 2 \times 2 = 4$
$D =
\begin{bmatrix}
8 & 0 & 2 & 1 \\
3 & -4 & 9 & 4\\
6 & 9 & 2 & 1
\end{bmatrix}
$
Matrix $D$ is a matrix and formed by $3$ rows and $4$ columns. Therefore, the order of the matrix is $3 \times 4$. It is read as three by four matrix.
The total number of elements in matrix $D = 3 \times 4 = 12$.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2023 Math Doubts, All Rights Reserved