Linear inequality in One variable with Greater than sign

Inequality

$x \,>\, a$

Introduction

When two quantities are compared, one quantity can be greater than the second quantity. The comparison between them is denoted by the greater than symbol in mathematics.

Let $a$ and $x$ denote the quantities. Assume that the value of $x$ is greater than $a$, which means they are not equal. So, the inequality between them is written mathematically as follows.

$x > a$

Let’s study this mathematical inequality to understand some properties of the literals $a$ and $x$.

1. The literal $a$ represents a value. It does not depend on anything. So, it is a constant.
2. The literal $x$ is not an independent like $a$ because its value always depends on the value of the literal $a$.
3. According to the inequality, the value of $x$ should be greater than the value $a$, which means the value of $x$ can be $a+1$, $a+2$, $a+3$, and so on. It clears that the literal $x$ represents a set of values. So, the literal $x$ is a variable.

Look at the following arithmetic inequality for better understanding.

$x > 6$

The value of $x$ must be greater than $6$. It means, the value of $x$ can be $7$, $8$, $9$ and so on.

Representation

The linear inequality in one variable $x$ greater than $a$ can be represented in three ways in mathematics.

Interval notation

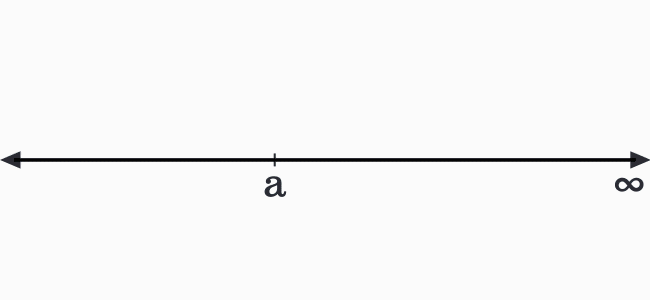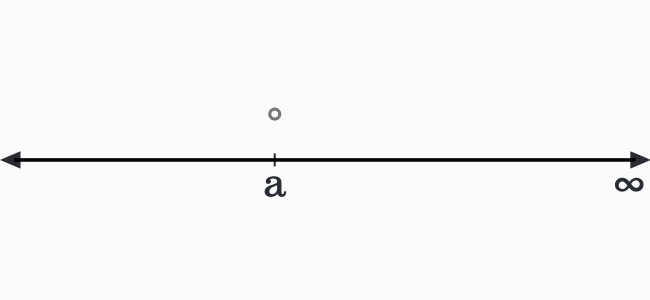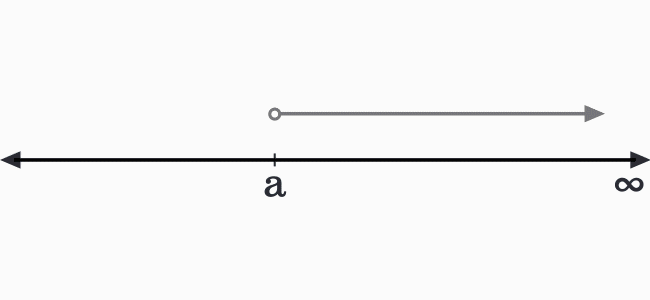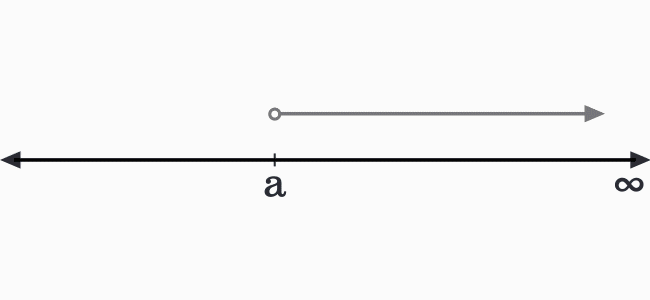
The value of $x$ is not equal to $a$ but every value after $a$ is equal to $x$. However, its last value cannot be determined. Hence, it is denoted by an infinity symbol mathematically.

The value of $x$ is not equal to $a$ and should not be equal to infinity. In other words, every value lies between $a$ and infinity belongs to the variable $x$.

Therefore, the solution set of $x$ is denoted as an open interval between $a$ and infinity.

$x \in (a,\,\infty)$

Set-Builder notation

In this example, the function is $x$ and its value is always greater than the value of $a$. Therefore, the solution set for $x$ greater than $a$ inequality is mathematically expressed in set builder form as follows.

$(1).\,\,\,$ $\{x \,|\, x \,>\, a\}$

$(2).\,\,\,$ $\{x \,:\, x \,>\, a\}$

Graphical notation

The $x$ is greater than $a$ linear inequality in one variable can be expressed graphically as per the one-dimensional cartesian coordinate system by a number line.

1. Take a number line and mark the position for the value $a$ on the number line.
2. The value of $a$ is not considered as a value of $x$ in this case and it is denoted by a hollow or open circle.
3. The values of $x$ after the value $a$ are connected by a straight line until it reaches the value of infinity.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.