Open interval

An interval that does not include the lower and higher values of a set is called an open interval.

Introduction

A set is a collection of members (elements) in which the quantity of one element is less than the remaining elements and the quantity another element is greater than the remaining elements. The remaining elements lie between the interval of lower and higher quantity elements.

In a special case, the interval has to be expressed by excluding the lower and higher quantity elements. Hence, it is called an open interval.

Let $x$ be a variable, $a$ and $b$ be two constants. There may be several values for $x$ but the value of $x$ is greater than $a$ but less than $b$.

$x > a$ and $x < b$

It means, all values of variable $x$ lie between $a$ and $b$ and it can be written mathematically as follows.

$a < x < b$

An open interval can be expressed in two different mathematical systems. So, let’s learn each system clearly.

Graphical Representation

The open interval can be represented by a graphical system and there are two steps to express it graphically.

1. The interval between the lower quantity ($a$) and the higher quantity ($b$) is represented by a line segment.
2. The left and right side endpoints of the line segment represent the lower and higher quantities of the set. In this case, the interval has to represent by excluding lower real quantity ($a$) and higher real quantity ($b$). Hence, each endpoint is denoted by a hollow or open circle.

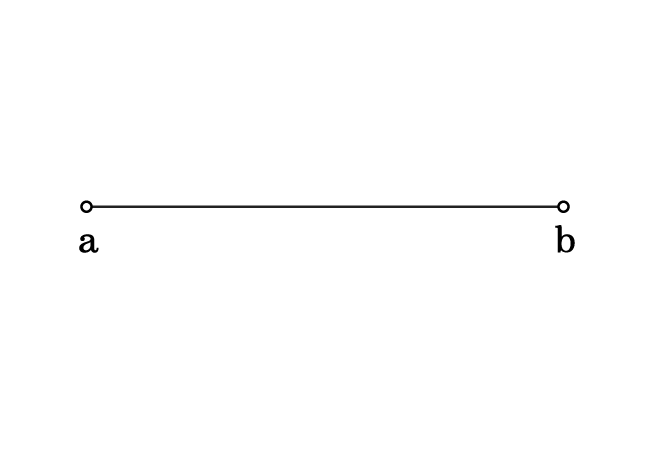
Thus, an open internal is expressed in the graphical system in mathematics.

Mathematical Representation

It is not convenient to express an open interval graphically more than once. Hence, the mathematical representation of an open interval was introduced in mathematics to write it easily.

An open interval between the quantities $a$ and $b$ is written mathematically as follows.

$\big(a, b\big)$

1. An interval is formed between the quantities $a$ and $b$. Hence, they are written in a row by separating them with a comma symbol.
2. The parentheses (or round brackets) are used to represent that we have to consider the values between $a$ and $b$ except the lower quantity $a$ and higher quantity $b$.

The open interval between $a$ and $b$ are the values of variable $x$ in this case. Hence, it can be written as follows.

$x \,∈\, \big(a, b\big)$

Thus, an open interval between any two quantities can be written mathematically in this way.

According to the set builder notation, an open interval between $a$ and $b$ is written in the following forms.

$(1).\,\,\,$ $\Big\{x \,\,|\,\, x \,∈\, R \,\, and \,\, a \, < \, x \, < \, b\Big\}$

$(2).\,\,\,$ $\Big\{x \,:\, x \,∈\, R \,\, and \,\, a \, < \, x \, < \, b\Big\}$

Example

$\big(2, 7\big)$

This mathematical expression represents the following two factors.

1. We should not take the numbers $2$ and $7$.
2. We have to consider the values between the numbers $2$ and $7$. For example, $3, 4, 5$ and $6$. Remember that not only these four values, we can also consider rational and irrational numbers between the numbers $2$ and $7$.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.