• Algebra
• Trigonometry
• Geometry
• Calculus

Slope and $\large y$ intercept form of a Line

Equation

$y \,=\, mx+c$

It is an equation of a straight line when a straight line intercepts $y$-axis at a point with some slope.

Proof

A straight line intercepts the vertical $y$-axis at point $B$ with an intercept $c$ and it makes an angle of $\theta$ with horizontal axis. The point $B$ in the form of coordinates is $B(0, c)$.

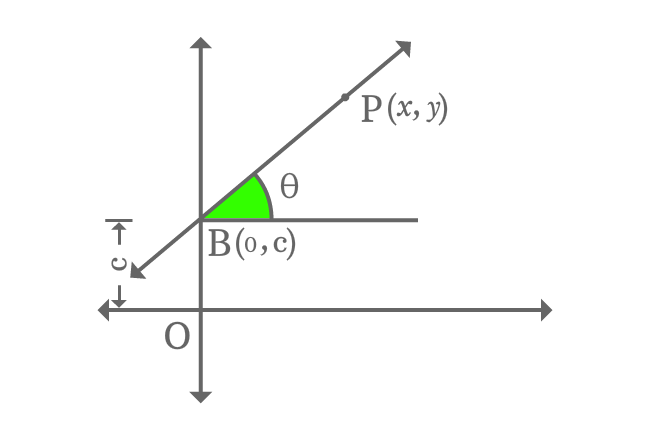
$P$ is a point on the straight line and it is $x$ and $y$ units distance from the origin in the directions of horizontal and vertical axes respectively. So, the point $P$ in the form of coordinates is written as $P(x, y)$.

Therefore, the straight line is denoted as $\small \overleftrightarrow{BP}$ in mathematics geometrically.

Take, the slope of straight line is represented by $m$ and write it in trigonometric form.

$m \,=\, \tan{\theta}$

Draw a perpendicular line to parallel line of $x$-axis from point $P$ and it intersects the parallel line of $x$-axis at point $Q$. Thus, a right triangle ($\Delta QBP$) is formed geometrically.

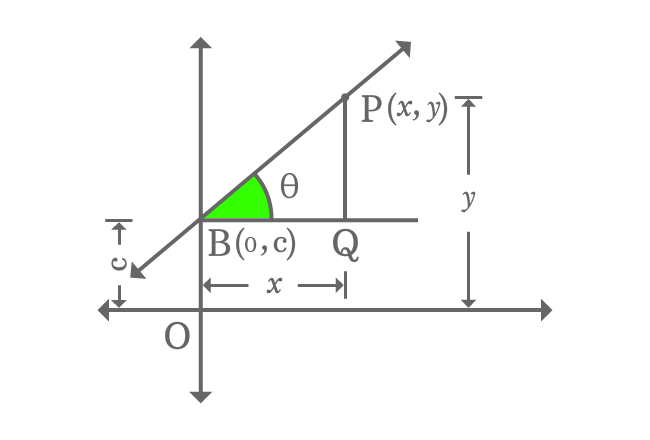
Now, find the $\tan{\theta}$ in trigonometric system and it equals to the slope of the straight line.

$\tan{\theta} \,=\, \dfrac{PQ}{BQ}$

$\implies \tan{\theta} \,=\, \dfrac{OP-OQ}{BQ}$

$\implies \tan{\theta} \,=\, \dfrac{y-c}{x}$

$\implies m \,=\, \dfrac{y-c}{x}$

$\implies mx \,=\, y-c$

$\implies mx+c \,=\, y$

$\,\,\, \therefore \,\,\,\,\,\, y \,=\, mx+c$

It is a linear equation which represents an equation of a straight line when a straight line intercepts $y$-axis with a $y$-intercept and slope. Therefore, it is called as slope and $y$-intercept form equation of a straight line.