Slope of a Straight Line in coordinates form

Equation

$m \,=\, \dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}$

The ratio between differences of ordinates and abscissae of any two points on a line is called slope of a straight line.

Introduction

$\overleftrightarrow{PQ}$ is a straight line with some inclination in Cartesian coordinate system.

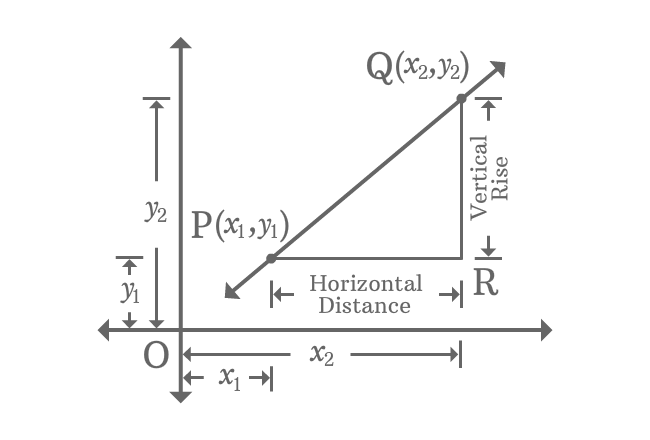
The coordinates of $P$ and $Q$ are $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$. Draw a parallel line to horizontal axis from point $P$ and also draw a perpendicular line to same axis from point $Q$. The two lines are intersected at point $R$.

The length of $\overline{QR}$ represents vertical rise of the points $P$ and $Q$ and the length of $\overline{PR}$ represents the horizontal distance between them. The ration between them is called gradient of the straight line and it is denoted by letter $m$.

$m \,=\, \dfrac{Vertical \, Rise}{Horizontal \, Distance}$

$\implies m \,=\, \dfrac{QR}{PR}$

$\implies m \,=\, \dfrac{OQ-OR}{OR-OP}$

$\,\,\, \therefore \,\,\,\,\,\, m \,=\, \dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}$

In this example, $x_{1}$ and $x_{2}$ are called abscissae and $y_{1}$ and $y_{2}$ are called ordinates geometrically.

It is proved that the slope of a straight line in terms of a coordinates is the ratio of differences of ordinates and abscissae of any two points on a line.