Proof of Internal Division Section formula

The internal division section formula is one kind of section formula. It is used to find the coordinates of a point which internally divides the line joining two points in a specific ratio.

$P(x, y)$ $\,=\,$ $\bigg(\dfrac{mx_2+nx_1}{m+n}, \dfrac{my_2+ny_1}{m+n}\bigg)$

It is called the internal division section formula in algebraic form and it can be derived in mathematical form by geometry. Now, let us learn how to derive the internal division section formula.

Geometric steps for Proving the section formula

Let’s imagine a line segment in a two dimensional space. The line segment is formed by joining two points $L$ and $M$. The point $P$ is a point on the line segment.

1. $x_1$ and $y_1$ are coordinates of the point $A$. So, the point $A$ is written in point form as $A (x_1, y_1)$ in mathematics.
2. $x_2$ and $y_2$ are two dimensional coordinates of the point $B$. Mathematically, the point $B$ is written in point form as $B (x_2, y_2)$.
3. $x$ and $y$ are the two cartesian coordinates of the point $P$. Hence, the point $P$ is written in point form as $P (x, y)$ in mathematics.
4. Assume that the point $P$ divides the line segment internally in a ratio of $m : n$

$\,\,\,\therefore\,\,\,\,\,\,$ $\dfrac{AP}{PB} \,=\, \dfrac{m}{n}$

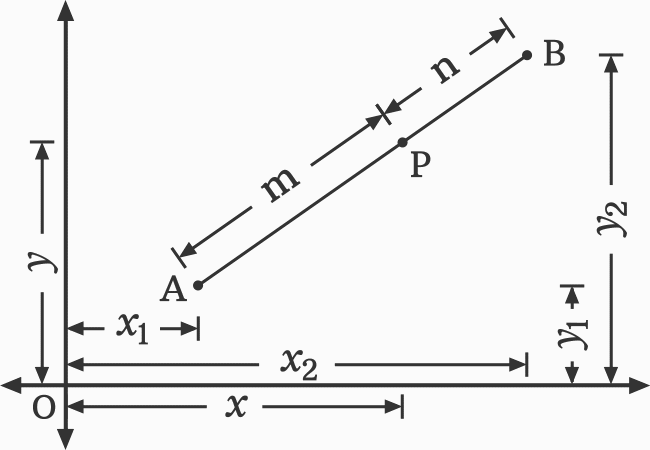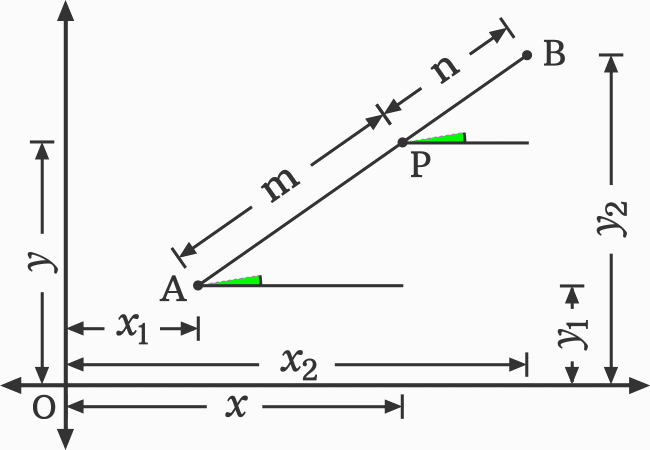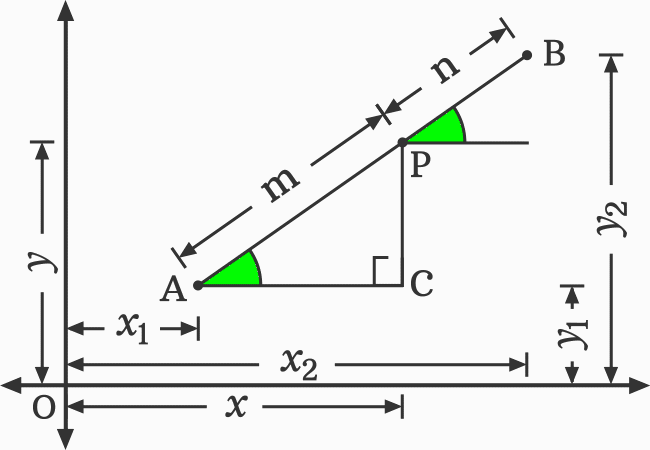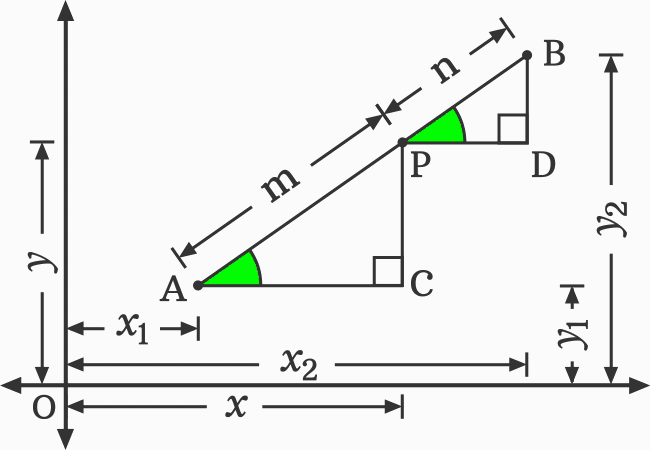
Now, let’s construct two triangles to carry the geometric procedure to next level.

1. Draw a horizontal line from point $A$ and also draw a horizontal line from point $P$.
2. Draw a vertical line from point $P$ to intersect the horizontal line at point $C$ perpendicular. Thus, it formed a right triangle $PAC$.
3. Similarly, draw a vertical line from point $B$ to intersect the horizontal line at point $D$ perpendicular. Thus, it formed a right angled triangle $BPD$.

In this way, we have constructed two triangles and they are written as $\Delta PAC$ and $\Delta BPD$ geometrically.

Finding the x coordinate of the Point

The angles of both triangles are equal geometrically. It means $\angle PAC \,=\, \angle BPD$. Hence, the two right triangles are similar triangles. It is written as $\Delta PAC$ $\sim$ $\Delta BPD$ in mathematics.

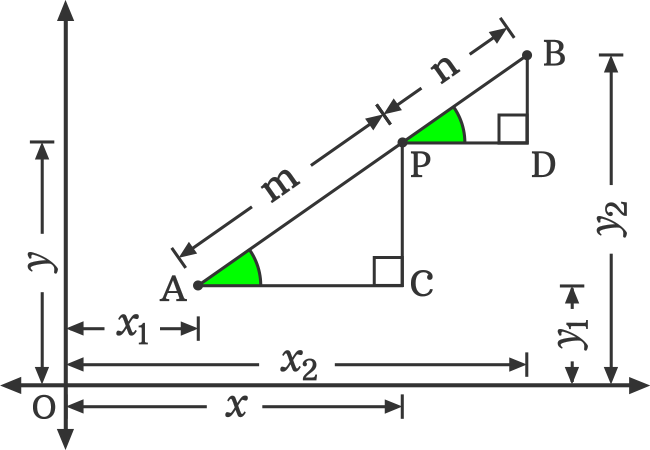
According to the similarity property of the triangles.

$\dfrac{AP}{AC} \,=\, \dfrac{PB}{PD}$

$\implies$ $\dfrac{AP}{PB} \,=\, \dfrac{AC}{PD}$

In this case

1. $AC$ $\,=\,$ $OC-OA$ $\,=\,$ $x-x_1$
2. $PD$ $\,=\,$ $OD-OP$ $\,=\,$ $x_2-x$

$\implies$ $\dfrac{m}{n} \,=\, \dfrac{x-x_1}{x_2-x}$

$\implies$ $m \times (x_2-x) \,=\, n \times (x-x_1)$

The factor can be distributed over the difference of the terms by the distributive property of multiplication over subtraction.

$\implies$ $m \times x_2$ $-$ $m \times x$ $\,=\,$ $n \times x$ $-$ $n \times x_1$

There are two like algebraic terms in this equation. So, write the like algebraic terms on one side of the equation and leave the unlike terms on the other side of the equation.

$\implies$ $m \times x_2$ $+$ $n \times x_1$ $\,=\,$ $m \times x$ $+$ $n \times x$

$\implies$ $m \times x$ $+$ $n \times x$ $\,=\,$ $m \times x_2$ $+$ $n \times x_1$

In the left hand side expression of the equation, $x$ is a common factor in both terms of the expression. So, it can be taken out common from the terms to simplify this equation further.

$\implies$ $x \times (m+n)$ $\,=\,$ $mx_2+nx_1$

Finally, shift the multiplying factor to the right hand side of the equation for finding the value of $x$.

$\,\,\,\therefore\,\,\,\,\,\,$ $x$ $\,=\,$ $\dfrac{mx_2+nx_1}{m+n}$

Finding the y coordinate of the Point

According to the similarity property of the $\Delta PAC$ and $\Delta BPD$.

$\dfrac{AP}{PC} \,=\, \dfrac{PB}{BD}$

$\implies$ $\dfrac{AP}{PB} \,=\, \dfrac{PC}{BD}$

In this case

1. $PC$ $\,=\,$ $OP-OC$ $\,=\,$ $y-y_1$
2. $BD$ $\,=\,$ $OB-OD$ $\,=\,$ $y_2-y$

$\implies$ $\dfrac{m}{n} \,=\, \dfrac{y-y_1}{y_2-y}$

This equation can be simplified by the cross multiplication technique.

$\implies$ $m \times (y_2-y) \,=\, n \times (y-y_1)$

On both sides of the equation, a factor is multiplying the difference of the terms. Each factor can be distributed across the subtraction by the distributive property of multiplication across subtraction.

$\implies$ $m \times y_2$ $-$ $m \times y$ $\,=\,$ $n \times y$ $-$ $n \times y_1$

In this algebraic equation, there are two like terms. So, move like algebraic terms to one side of the equation and move the unlike terms to the other side of the equation.

$\implies$ $m \times y_2$ $+$ $n \times y_1$ $\,=\,$ $m \times y$ $+$ $n \times y$

$\implies$ $m \times y$ $+$ $n \times y$ $\,=\,$ $m \times y_2$ $+$ $n \times y_1$

There is a common factor in both terms of the left hand side expression of the equation. It can be taken out common from both the like terms.

$\implies$ $y \times (m+n)$ $\,=\,$ $my_2+ny_1$

For calculating the value of $y$ coordinate, move the multiplying factor to the right hand side of the equation.

$\,\,\,\therefore\,\,\,\,\,\,$ $y$ $\,=\,$ $\dfrac{my_2+ny_1}{m+n}$

Express the coordinates in Point form

We have taken that $x$ and $y$ are two coordinates of the point $P$. The $x$ coordinate of the point $P$ is derived geometrically in mathematical form in the second step.

$x$ $\,=\,$ $\dfrac{mx_2+nx_1}{m+n}$

Similarly, the $y$ coordinate of the point $P$ is derived in algebraic form in the third step geometrically.

$y$ $\,=\,$ $\dfrac{my_2+ny_1}{m+n}$

In mathematics, the point P with its coordinates is written in point form as $P(x,y)$.

$\,\,\,\therefore\,\,\,\,\,\,$ $P(x, y)$ $\,=\,$ $\bigg(\dfrac{mx_2+nx_1}{m+n}, \dfrac{my_2+ny_1}{m+n}\bigg)$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.