Internal Division Section formula
Fact-checked:
Formula
$P(x, y)$ $\,=\,$ $\bigg(\dfrac{mx_2+nx_1}{m+n}, \dfrac{my_2+ny_1}{m+n}\bigg)$
A formula that helps us to find the coordinates of a point which internally divides the line joining two points in a specific ratio is called the internal division section formula.
Introduction
A point on a line segment divides the line internally in a specific ratio. The coordinates of the point on the line segment can be evaluated from the coordinates of the both endpoints of that line and the internal division ratio.
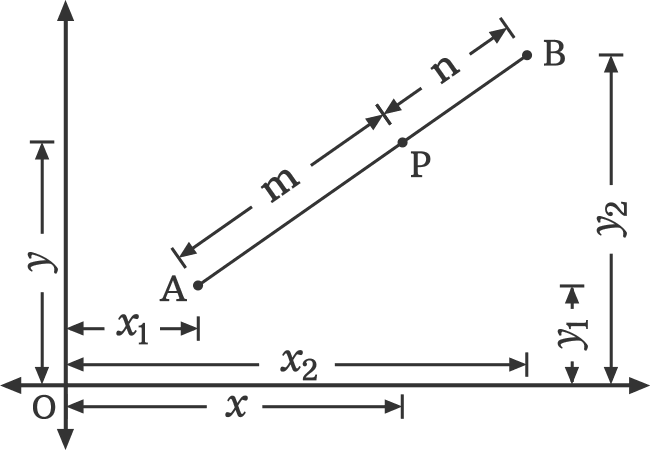
Let $x_1$ and $y_1$ be coordinates of one endpoint of the line segment and $x_2$ and $y_2$ be coordinates of another endpoint of the line segment in a two dimensional cartesian coordinate system.
If $x$ and $y$ are the coordinates of the point which internally divides the line in a ratio of $m : n$, then the coordinates of the point can be calculated from the below formula.
$P(x, y)$ $\,=\,$ $\bigg(\dfrac{mx_2+nx_1}{m+n}, \dfrac{my_2+ny_1}{m+n}\bigg)$
This formula is called the internal division section formula.
Proof
Learn how to derive the internal division section formula in algebraic form geometrically.
Problems
The list of geometry problems with solutions to learn how to find the coordinates of a point which internally divides a line in a given ratio by using the internal division section formula.

