Scalene Triangle

A triangle that has three unequal sides is called a scalene triangle.

Introduction

According to English language, the word “scalene” means unequal sides in length.

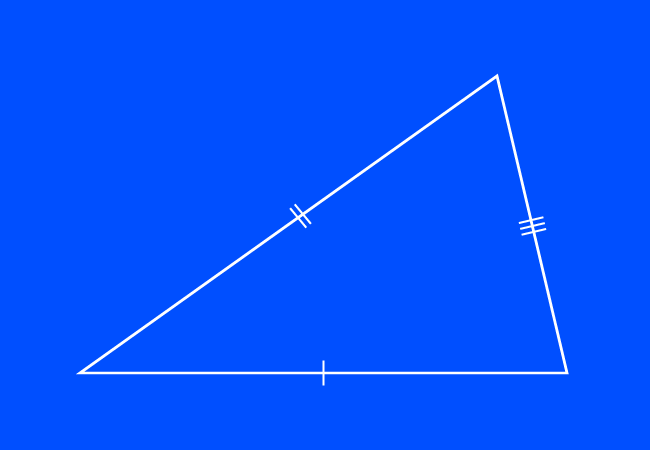
A triangle is geometrically formed by connecting three line segments. The lengths of all three sides can be different in some cases. The word scalene is added to triangle for calling such triangles, in which the lengths of all three sides are different. Hence, those triangles are called as scalene triangles in geometry.

Graphically, a scalene triangle is represented by drawing one, two and three small perpendicular lines to sides of the triangle at their middle point.

Due to the inequality property of sides in scalene triangles, the interior angles of any scalene triangle are also unequal.

Construction

Let’s construct the scalene triangle for studying it further.

1. Draw a line from point $O$ to $P$ horizontally by a ruler. In this case, the length of this horizontal line segment is $8\,cm$.
2. Take compass and set the distance between point and pencil point to some length. In this case, it is set to $10\,cm$ by the reference of a ruler. Now, draw an arc on the plane from point $O$.
3. Similarly, set the compass to another length. Here, it is set to $5\,cm$ and then draw an arc from point $P$ but it must intersect the previously drawn arc for completing the construction of scalene triangle.

In this way, a triangle is constructed geometrically in three steps. In mathematics, it is simply written as $\Delta POQ$.

Properties

We can now study the properties of the scalene triangle from the above constructed triangle.

Sides

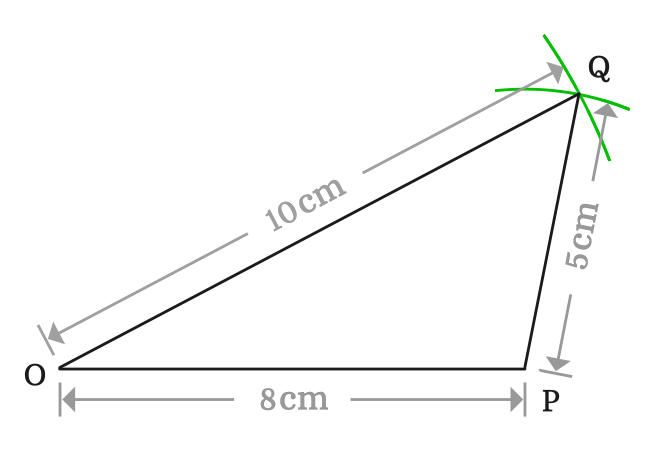
Let’s list the lengths of all three sides of this triangle.

$(1).\,\,\,$ The length of the side $\overline{OP}$ is $OP \,=\, 8\,cm$

$(2).\,\,\,$ The length of the side $\overline{OQ}$ is $OQ \,=\, 10\,cm$

$(3).\,\,\,$ The length of the side $\overline{PQ}$ is $PQ \,=\, 5\,cm$

In $\Delta POQ$, the lengths of all three sides are not equal. Hence, this triangle is called as a scalene triangle geometrically. Therefore, it is cleared that a triangle is called as a scalene triangle when lengths of all its sides are not equal.

$\therefore \,\,\,\,\,\,$ $OP$ $\,\ne\,$ $OQ$ $\,\ne\,$ $PQ$

Angles

Now, measure the angles of the triangle $POQ$ by a protractor.

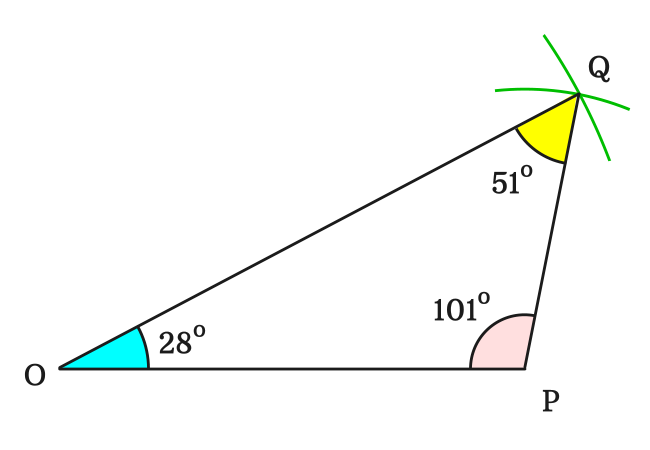
It is measured that

$(1).\,\,\,$ $\angle QOP \,=\, 28^°$

$(2).\,\,\,$ $\angle OPQ \,=\, 101^°$

$(3).\,\,\,$ $\angle PQO \,=\, 51^°$

We can observe that the three angles are unequal.

$\therefore \,\,\,\,\,\,$ $\angle QOP$ $\,\ne\,$ $\angle OPQ$ $\,\ne\,$ $\angle PQO$

In any scalene triangle, the angles are unequal due to the unequal sides of the triangle.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.