Isosceles Triangle

A triangle that has two sides of equal length is called an isosceles triangle.

Introduction

According to English language, the word “isosceles” means two sides of equal length.

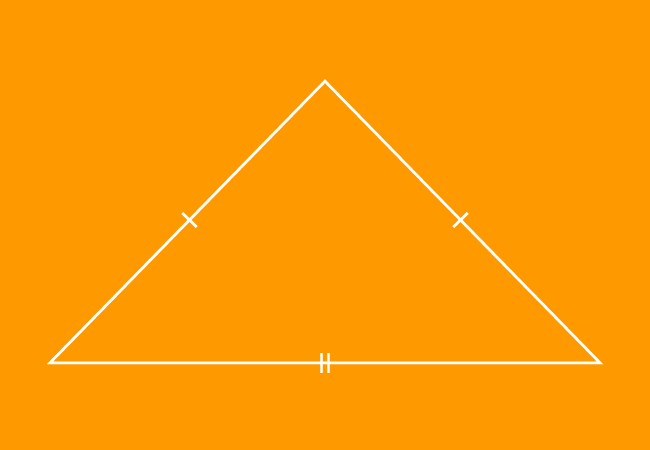
Geometrically, a triangle is formed by connecting the endpoints of three line segments. In some triangles, the lengths of any two sides can be same. Hence, the word “isosceles” is added to triangle for expressing such triangles, in which the lengths of two sides are equal. Hence, the triangles are called as isosceles triangles in geometry.

An isosceles triangle is represented graphically by drawing one and two small perpendicular lines to sides of the triangle at their middle points.

Due to the equality property of sides in isosceles triangles, the two interior angles of any isosceles triangle are equal.

Construction

Let’s learn how to construct an isosceles triangle and it is useful to study its properties.

1. Draw a line segment from point $C$ to $D$ horizontally by using a ruler. Here, the length of horizontal line segment is $9\,cm$.
2. Set the distance between point and pencil point of compass to some length by the reference of a ruler. In this case, it is set to $7\,cm$. Then, draw an arc on the plane from point $C$.
3. Similarly, draw another arc from point $D$ with same length by the compass but it should intersect the previously drawn arc in order to complete the construction of an isosceles triangle.

Thus, a triangle can be constructed geometrically in three simple steps and it is simply expressed as $\Delta ECD$ in mathematics.

Properties

The properties of an isosceles triangle can be studied from the above constructed triangle.

Sides

Now, list the lengths of all three sides of the triangle $ECD$.

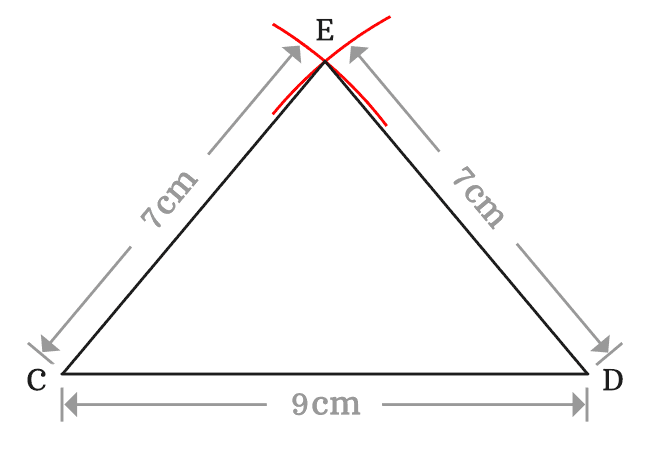
$(1).\,\,\,$ The length of the side $\overline{CD}$ is $CD \,=\, 9\,cm$

$(2).\,\,\,$ The length of the side $\overline{CE}$ is $CE \,=\, 7\,cm$

$(3).\,\,\,$ The length of the side $\overline{DE}$ is $DE \,=\, 7\,cm$

In $\Delta ECD$, the lengths of two sides are equal but the length of third side is different. Hence, the triangle is called as an isosceles triangle geometrically. So, it is cleared that a triangle is called as an isosceles triangle when the lengths of any two sides are equal.

$\therefore \,\,\,\,\,\,$ $CD$ $\,\ne\,$ $CE$ $\,=\,$ $DE$

Angles

For studying the property of angles, measure the angles of triangle $ECD$ by a protractor.

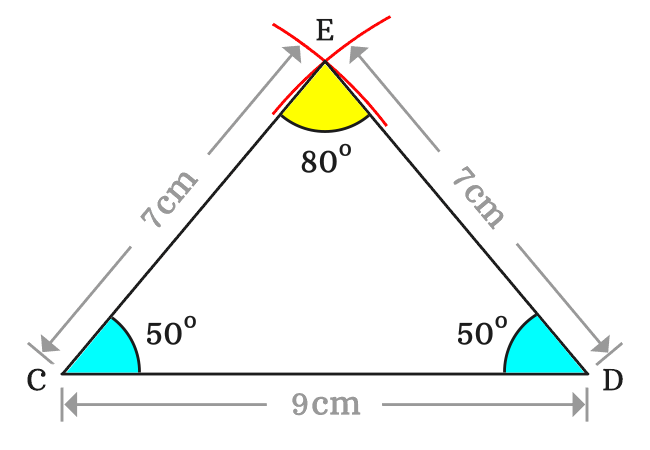
It is measured that

$(1).\,\,\,$ $\angle CED \,=\, 80^°$

$(2).\,\,\,$ $\angle ECD \,=\, 50^°$

$(3).\,\,\,$ $\angle CDE \,=\, 50^°$

It is cleared that the two angles are equal but third angle is different.

$\therefore \,\,\,\,\,\,$ $\angle CED$ $\,\ne\,$ $\angle ECD$ $\,=\,$ $\angle CDE$

In isosceles triangle, the two angles are equal because of the two equal sides of the triangle.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.