Product identity of Cosine and Secant functions

Formula

$\cos{\theta}\sec{\theta} \,=\, 1$

Proof

Mathematically, the cosine and secant functions are reciprocals. So, their product must be equal to one and the product relation between cos and sec functions can also be proved in trigonometry.

$\Delta RPQ$ is a right triangle and its angle is assumed as theta ($\theta$).

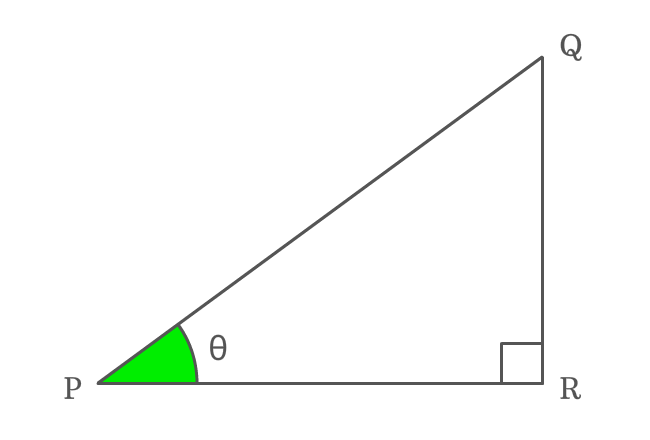
Write Cos function in ratio form

Write cosine function ($\cos{\theta}$) in its ratio form firstly.

$\cos{\theta} \,=\, \dfrac{PR}{PQ}$

Write Sec function in ratio form

Now, write secant function ($\sec{\theta}$) in its ratio form.

$\sec{\theta} \,=\, \dfrac{PQ}{PR}$

Evaluate Product of Cosine and Secant

Finally, multiply both cosine and secant functions to find the product of them.

$\cos{\theta} \times \sec{\theta}$ $\,=\,$ $\dfrac{PR}{PQ} \times \dfrac{PQ}{PR}$

$\implies$ $\cos{\theta} \times \sec{\theta}$ $\,=\,$ $\dfrac{PR \times PQ}{PQ \times PR}$

$\implies$ $\cos{\theta} \times \sec{\theta}$ $\,=\,$ $\require{cancel} \dfrac{\cancel{PR} \times \cancel{PQ}}{\cancel{PQ} \times \cancel{PR}}$

$\,\,\, \therefore \,\,\,\,\,\,$ $\cos{\theta}.\sec{\theta} \,=\, 1$

Therefore, it has proved that the product of cos and sec functions at an angle is equal one, and this property in trigonometry is used as a formula in mathematics.

Note

Keep one thing in your mind always that the angle of a right triangle can be represented by any symbol but the product of cosine of angle and secant of angle always equals to one.

For example, if $x$ denotes angle of right triangle, then

$\cos{x}.\sec{x} \,=\, 1$

Similarly, if $A$ is used to represent angle of right triangle, then

$\cos{A}.\sec{A} \,=\, 1$

The cosine and secant functions in the trigonometric product identity can be expressed in terms of any angle but the product of them equals to one mathematically.