Coordinates of a Point in Two dimensional space

The horizontal and vertical distances of a point from the origin in two dimensional space are called the coordinates of a point.

Introduction

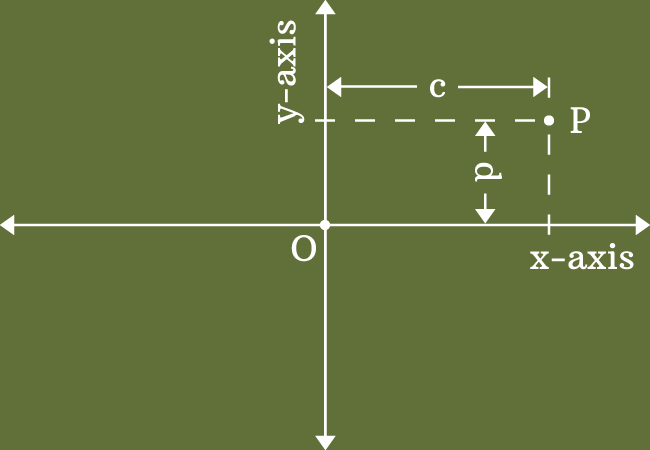
The two dimensional Cartesian coordinate system is formed in geometry by the perpendicular bisection of two number lines. So, every point can be measured from the origin in two perpendicular directions on the basis of both number lines of coordinate axes.

Each distance of a point is called the coordinate of the point. Therefore, a point has two coordinates in two dimensional rectangular Cartesian coordinate system and the two coordinates of a point are expressed by two special names in geometric system.

Abscissa

The horizontal distance of a point from origin in two dimensional space is called the $x$-coordinate or abscissa.

Ordinate

The vertical distance of a point from origin in bi-dimensional space is called the $y$-coordinate or ordinate.

Representation

In two dimensional coordinate geometry, a point with its coordinates are simply expressed in ordered pair form.

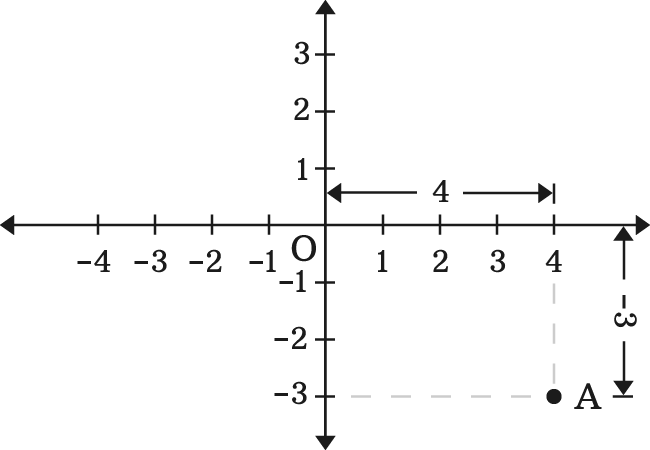
The abscissa and ordinate of a point are written in a row inside parenthesis with comma separation but the $x$-coordinate should be first and then $y$-coordinate.

Example

Let $A$ be a point in the coordinate plane. Its $x$ coordinate is $4$ and $y$ coordinates is $-3$.

The coordinates of the point $A$ are written in coordinate geometry as $(4, -3)$.