Complete angle

Definition

An angle of $360^\circ$ is called a complete angle.

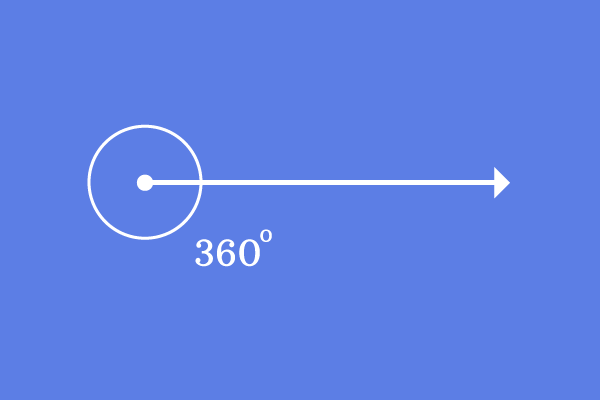
A straight line makes an angle of $360^\circ$ to reach its initial position completely by the rotation. Hence, the angle is called as the complete angle.

A complete angle is represented same as the zero angle but there is one difference between them and it is the amount of rotation.

Representation

The complete angle is represented in three different angle measuring systems.

1. It is denoted by $360^°$ in Sexagesimal system
2. It is denoted by $2\pi$ in Circular system
3. It is denoted by $400^g$ in Centesimal system

Formation

There are two possibilities to form complete angles in geometric system.

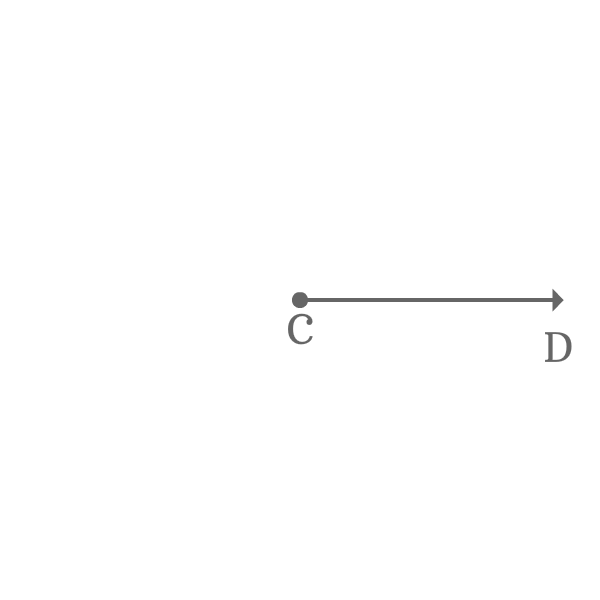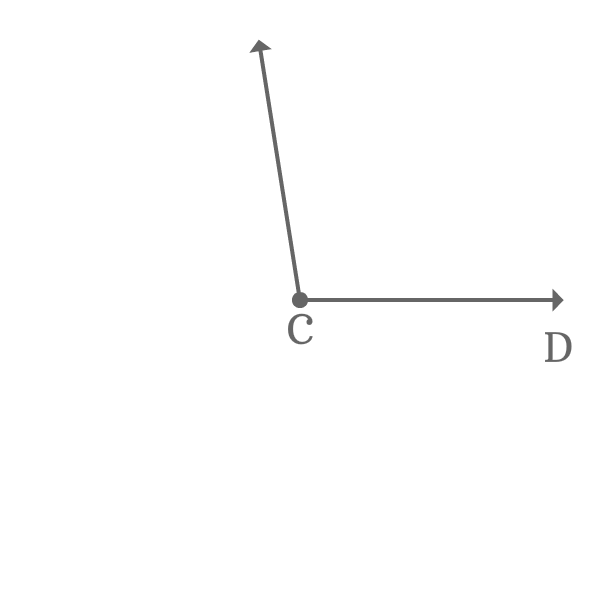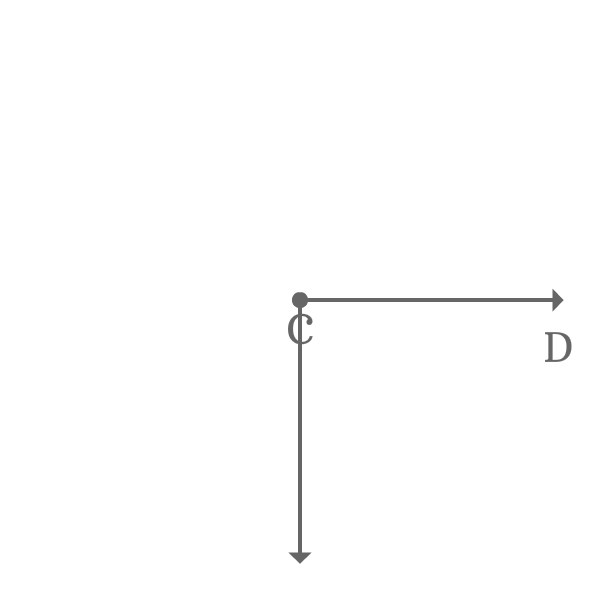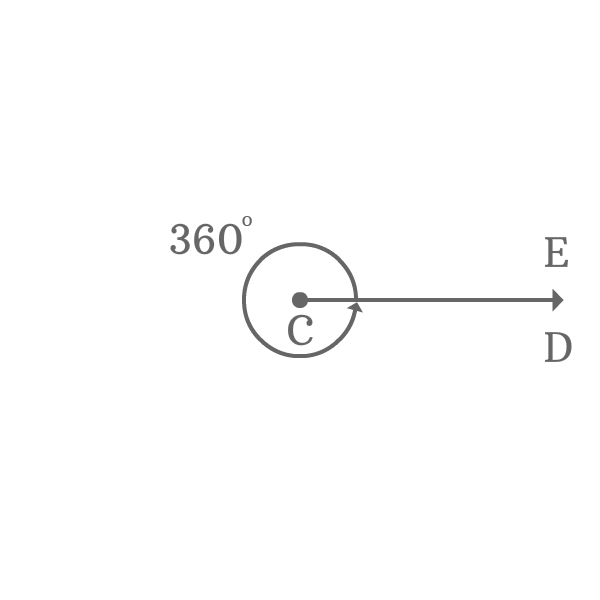
$\overrightarrow{CD}$ is a ray and it is initially at a position on the plane.

The ray $\overrightarrow{CD}$ is rotated an angle of $360^\circ$ to reach the same position where the same ray is called as $\overrightarrow{CE}$.

The angle made by the ray to reach its final position from its initial position is $\angle ECD$ and the amount of rotation is $360^\circ$.

$\angle ECD = 360^\circ$

The angle $ECD$ is $360^\circ$. So, the angle $ECD$ is an example for the complete angle.

$\overrightarrow{FG}$ is a ray and $\overrightarrow{FH}$ is another ray. The two rays make same angle but the angle between them is a complete angle.

The angle between them is denoted by $\angle GFH$.

$\angle GFH = 360^\circ$

Therefore, the angle $GFH$ is another example of a complete angle.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.