Complementary angles

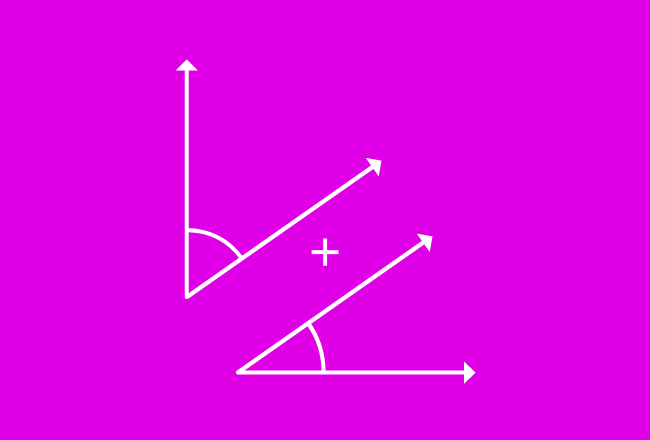
The angles whose sum equals to $90^\circ$ are called the complementary angles.

Introduction

Complementary angles are angles basically but the sum of them represents a right angle when the angles are added to each other.

One angle is known as complement of another angle and vice-versa.

Formula

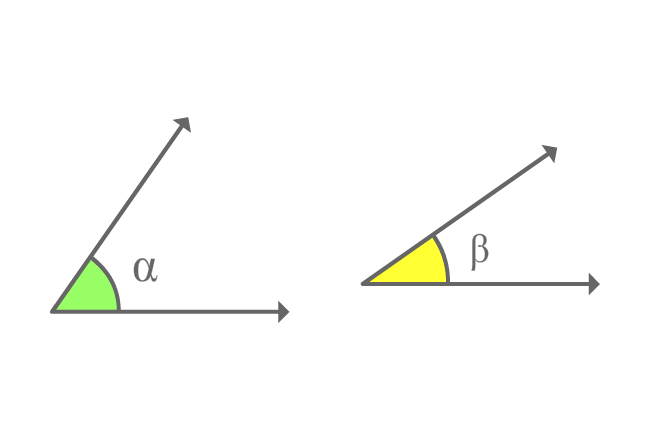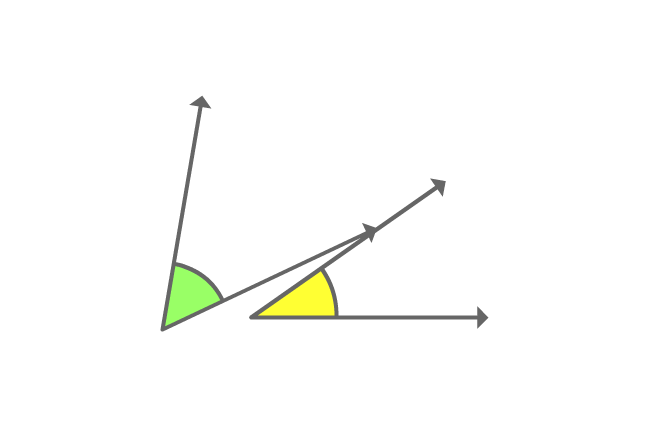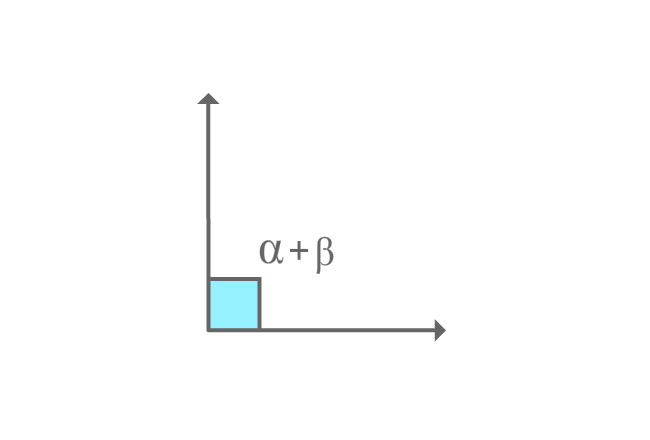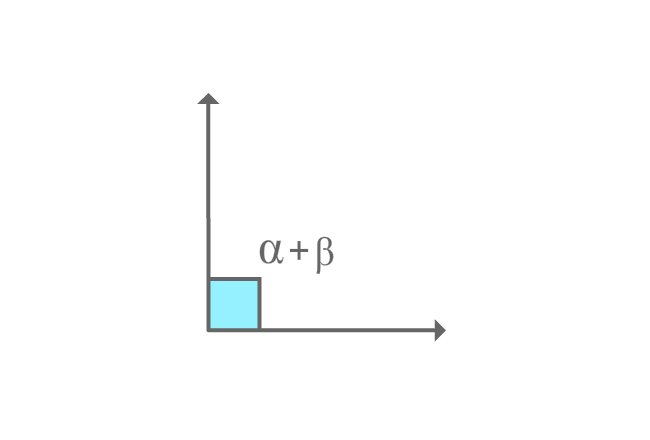
$\alpha$ and $\beta$ are two angles. The sum of them forms a right angle geometrically.

$\alpha+\beta = 90^\circ$

1. $\alpha$ is called complement of $\beta$
2. $\beta$ is called complement of $\alpha$

The angles $\alpha$ and $\beta$ are known as complementary angles.

Example

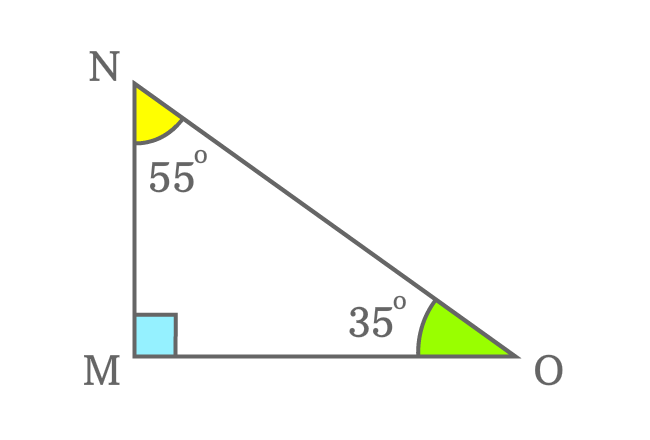
$\Delta MON$ is a right triangle.

It has three interior angles. One angle ($\angle OMN$) is right angle. The other two angles are $\angle MNO$ and $\angle NOM$.

The $\angle MNO$ is $55^\circ$ and the $\angle NOM$ is $35^\circ$. Now, add both angles.

$\angle MNO + \angle NOM$ $=$ $55^\circ + 35^\circ$

$\implies$ $\angle MNO + \angle NOM$ $=$ $90^\circ$

The sum of two angles is right angle $\Big(\dfrac{\pi}{2}\Big)$. Therefore, the angles ($\angle MNO$ and $\angle NOM$) are called as complementary angles.

The $\angle MNO$ is called as complement of the $\angle NOM$. Similarly, $\angle NOM$ is called as complement of the $\angle MNO$.