Cofunction identity of tan function

Formula

Sexagesimal System
$\tan{(90^\circ-\theta)} \,=\, \cot{\theta}$
Circular (or) Radian System
$\tan{\Big(\dfrac{\pi}{2}-x\Big)} \,=\, \cot{x}$

In this trigonometric rule, theta is used to represent angle in degrees and x is used to represent angle in radians.

Tan function contains an allied angle which belongs to first quadrant. So, the formula is called as first quadrant’s allied angle identity of tan function. Similarly, the angles of both tan and cot functions are complementary angles. Therefore, it is usually called as cofunction identity of tan function.

Proof

In first quadrant, a line segment is rotated to an angle and the line segment is called as $\overline{PQ}$.

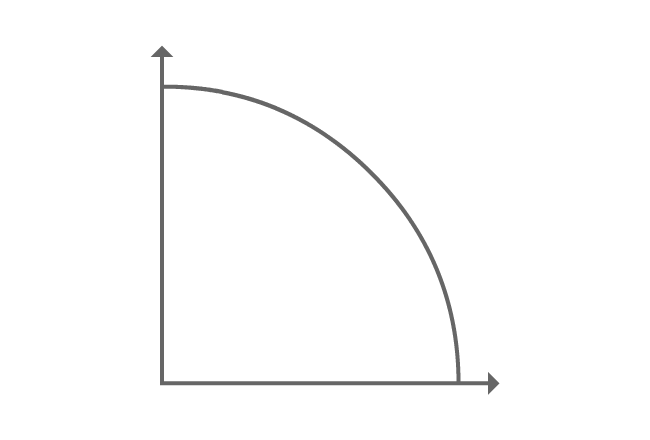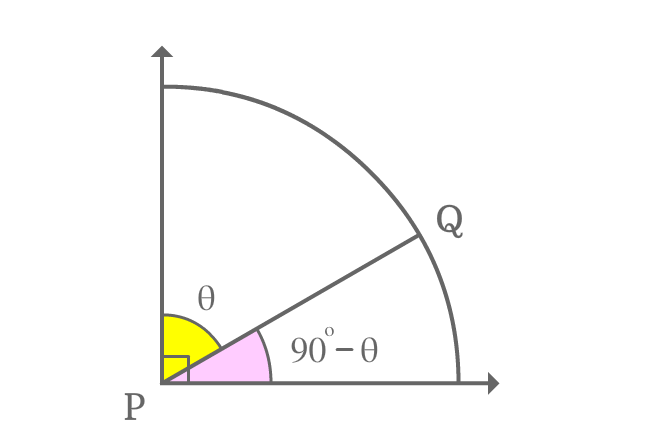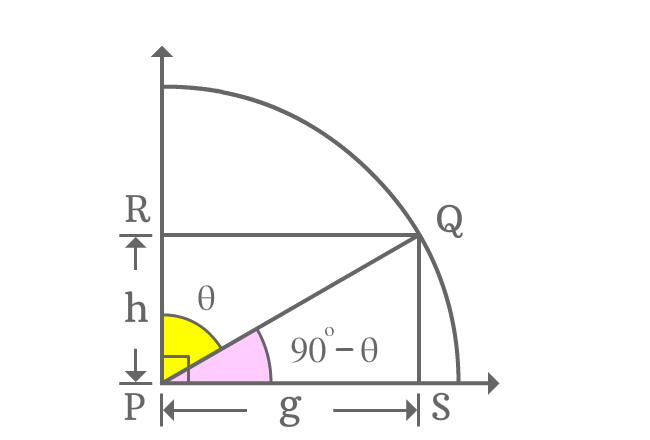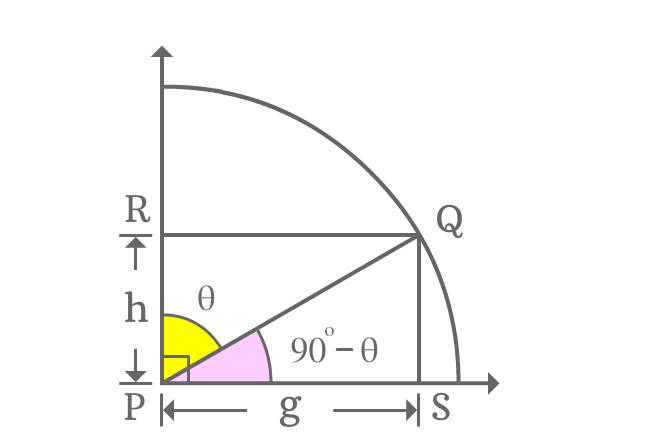
Perpendicular lines are drawn to horizontal and vertical lines from point $Q$ and they intersect perpendicular rays at points $S$ and $R$ respectively. Thus, it constructed two right angled triangles geometrically, known as $\Delta QPR$ and $\Delta QPS$.

Assume $\angle QPR = \theta$, then $\angle QPS = 90^\circ-\theta$.

Assume $PS = g$, then $RQ = g$ and if $RP = h$, then $QS = h$ because of equality and parallelism of the line segments.

Express tan of allied angle

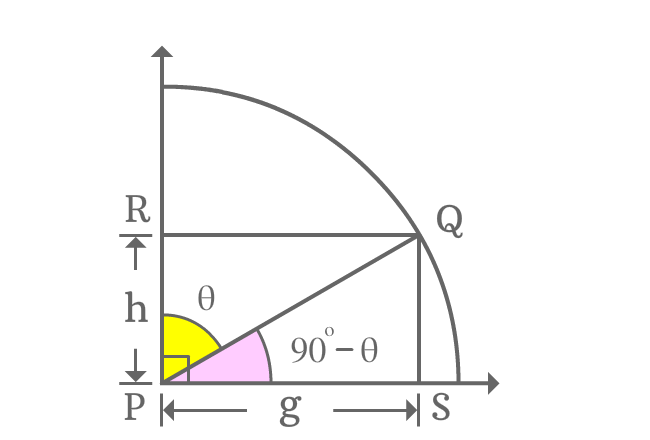
The angle of $\Delta QPS$ is an allied angle and it is $90^\circ-\theta$. Express tan of first quadrant’s allied angle in mathematical form by expressing it in the form of ratio of the associated sides.

$\tan{(90^\circ-\theta)} = \dfrac{QS}{PS}$

The lengths of both opposite and adjacent sides are known, and they are $h$ and $g$ respectively.

$\implies \tan{(90^\circ-\theta)} = \dfrac{h}{g}$

Find equivalent value of the fraction

Tan of allied angle of first quadrant is expressed as a fraction of the lengths of the sides and express the same fraction as an equivalent trigonometric function. It is possible by the $\Delta QPR$.

$\dfrac{h}{g} = \dfrac{PR}{QR}$

As per $\Delta QPR$, the angle of the triangle is theta. The ratio of lengths of $\overline{PR}$ to $\overline{QR}$ is cot of angle theta.

$\implies \dfrac{h}{g} = \cot{\theta}$

Cofunction identity of tan function

The previous two steps have proved geometrically that

$\tan{(90^\circ-\theta)}$ $=$ $\dfrac{h}{g}$ $=$ $\cot{\theta}$

$\therefore \,\,\,\,\,\, \tan{(90^\circ-\theta)} \,=\, \cot{\theta}$

Geometrically, it is proved that tan of first quadrant’s allied angle is equal to cot of angle. Hence, this trigonometric identity is known as first quadrant’s allied angle identity of tan function. But, the angles of both tan and cot functions are complementary angles. Due to this reason, this rule is known as cofunction identity of tan function.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.