Circular sector

The part of a circle enclosed by an arc and two radii is called a circular sector.

Introduction

Two different points on the circumference of a circle can be connected to the center (or centre) of the circle by drawing a line segment. Each line segment is geometrically known as the radius of the circle.

The circle can be divided into two portions by cutting through the two radii. Each part of the circle is called a circular sector and it is also called by the following two names in geometry.

1. Circle sector
2. Sector of a circle

The intersection of two arcs and two radii divides the entire circle into two parts and each part is known as a sector of the circle.

Classification

The sectors of a circle is classified into two types based on the amount of area enclosed by the arc and two radii.

1. Minor sector
2. Major sector

In this example, The point $C$ represents the centre (or center) of the circle. Let $P$ and $Q$ be any two points on the circumference of the circle. They can be connected to the center (or centre) by a line. The circle can be split into two parts by cutting through the two radii $\overline{CP}$ and $\overline{CQ}$.

Here, the points $R$ and $S$ are any two points on the circumference of the circle. They are actually considered to express the difference between both sectors in mathematical form.

Minor sector

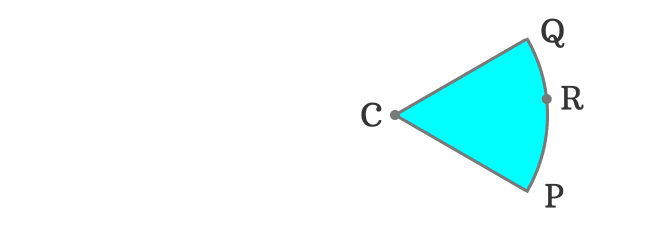
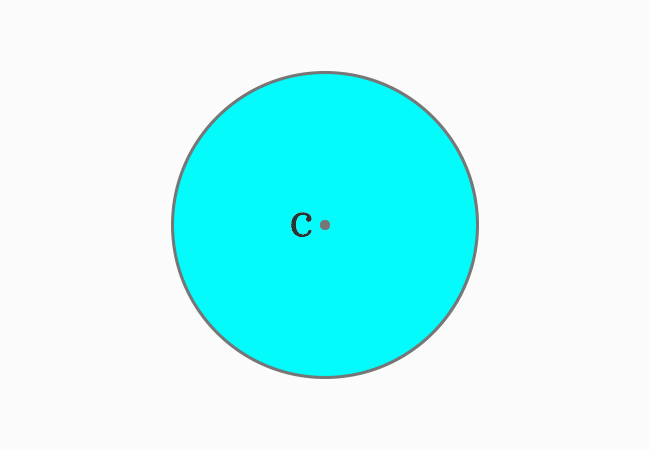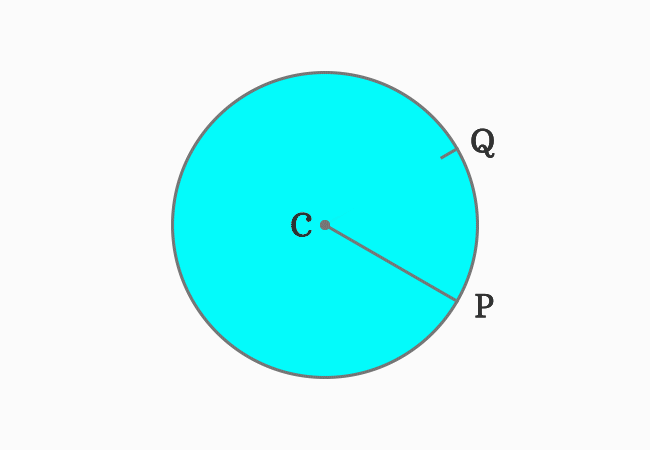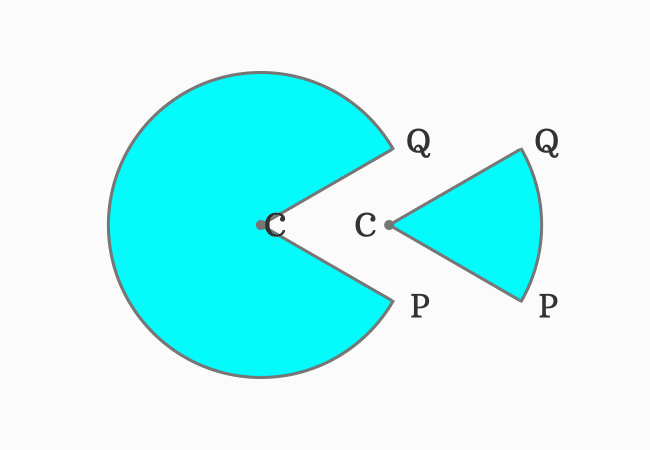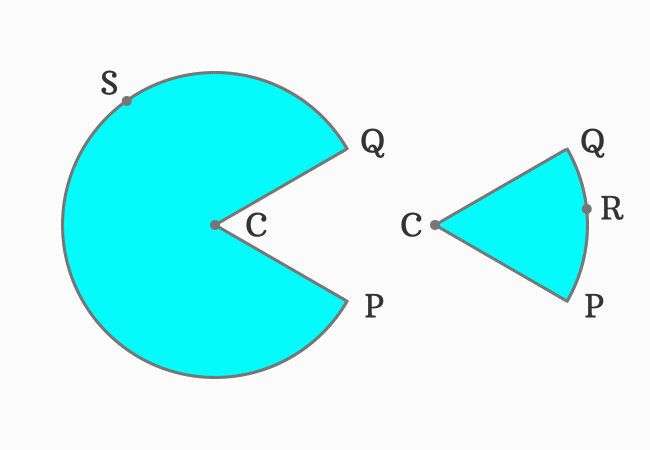
A portion from the circle is separated. It is formed by an arc $\stackrel{\Huge ⌢}{PRQ}$ and two radii $\overline{CP}$ and $\overline{CQ}$.

The area bounded by an arc $\stackrel{\Huge ⌢}{PRQ}$ and two radii $\overline{CP}$ and $\overline{CQ}$ is small. Hence, it is called the minor sector of the circle.

Major sector

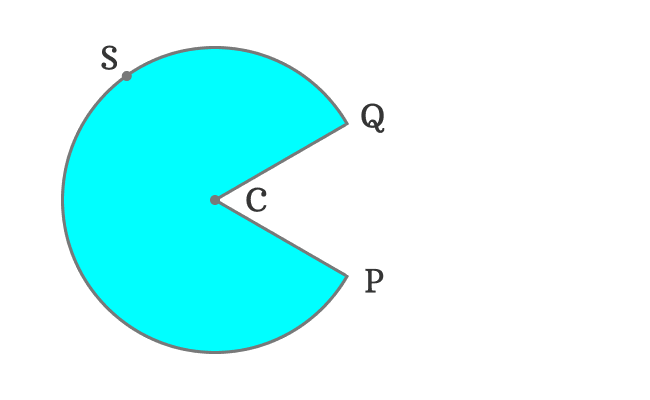
Another portion from the circle is separated. It is formed by an arc $\stackrel{\Huge ⌢}{PSQ}$ and two radii $\overline{CP}$ and $\overline{CQ}$.

The area bounded by an arc $\stackrel{\Huge ⌢}{PSQ}$ and two radii $\overline{CP}$ and $\overline{CQ}$ is big when compared to the previous case. Hence, the big portion of the circle is called the major sector of the circle.

Representation

A sector of the circle is expressed in mathematical form by following its geometric formation.

In this example, the minor sector is formed by an arc $\stackrel{\Huge ⌢}{PRQ}$ and two radii $\overline{CP}$ and $\overline{CQ}$. Hence, we have to involve all the points in them. Therefore, the minor sector is written as $\operatorname{sector} CPRQ$ in mathematics.

The major sector is formed by an arc $\stackrel{\Huge ⌢}{PSQ}$ and two radii $\overline{CP}$ and $\overline{CQ}$. Hence, we have to involve all the points in them. So, the major sector is written as $\operatorname{sector} CPSQ$ in mathematics.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.