Proof for Equation of a Circle when the circle touches the x-axis

The equation of a circle when the circle touches the x axis is expressed in one of the below two mathematical forms.

$(1).\,\,\,$ $(x-a)^2+(y-b)^2 \,=\, b^2$

$(2).\,\,\,$ $(x-h)^2+(y-k)^2 \,=\, k^2$

Let’s learn how to derive the equation of a circle geometrically in mathematical form when the circle is touching the $x$-axis in two dimensional cartesian coordinate system.

Construct a Triangle inside a Circle in a Quadrant

A right triangle (or right-angled triangle) has to construct inside a circle when the circle touches the $x$-axis at a point in a quadrant of the two-dimensional space and it is used to derive a circle’s equation in mathematical form when the circle is touching the $x$-axis at a point.

1. Let’s consider the first quadrant of two dimensional cartesian coordinate system. A circle is drawn in such a way that it touches the $x$ axis at a point.
2. Assume that the center (or centre) of a circle is denoted by $C$ and it is $a$ and $b$ units away from the origin in horizontal and vertical directions. Therefore, the centre (or center) in coordinate form is written as $C(a, b)$ in mathematics.
3. Similarly, $P$ is a point on the circumference and it is $x$ and $y$ units away from the origin in horizontal and vertical directions. Hence, it is written as $P(x, y)$ in coordinate form in geometric mathematics.
4. Connect the center $C$ and point $P$ by a line segment. The line segment $\overline{CP}$ represents the radius of the circle and its length is $r$ units. Now, draw a horizontal line from centre $C$ and also draw a vertical line from point $P$ towards $x$ axis in such a way that they got intersected at point $Q$. Thus, a right triangle $\Delta PCQ$ is constructed geometrically.

Evaluate the Length of each side of Triangle

In $\Delta PCQ$, $\overline{PQ}$, $\overline{CQ}$ and $\overline{CP}$ are opposite side, adjacent side and hypotenuse, and their lengths are written as $PQ$, $CQ$ and $CP$ respectively.

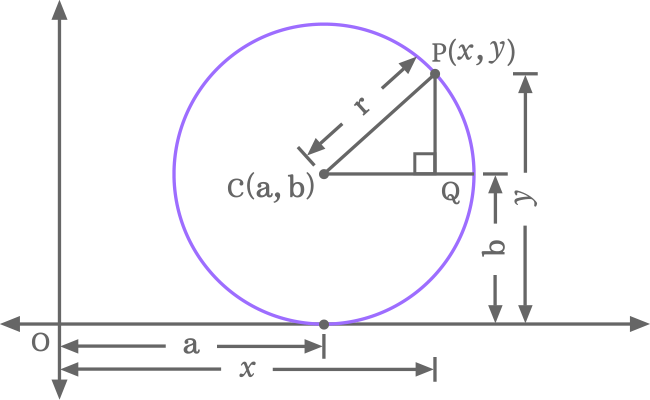
It is time to evaluate the length of each side of this triangle in algebraic form.

1. $CQ$ $\,=\,$ $OQ\,–\,OC$ $\,=\,$ $x \,–\,a$
2. $PQ$ $\,=\,$ $OP\,–\,OQ$ $\,=\,$ $y\,-\,b$
3. $CP \,=\, r$.

Express the mathematical Relation between them

We have successfully evaluated the length of each side of the right angled triangle in mathematical form. The relationship between the sides can be expressed mathematically by applying the Pythagorean Theorem to $\Delta QCP$.

${CP}^2$ $\,=\,$ ${CQ}^2+{PQ}^2$

Substitute the lengths of all three sides in the above equation.

$r^2$ $\,=\,$ $(x \,-\, a)^2$ $+$ $(y \,-\, b)^2$

$\,\,\,\therefore\,\,\,\,\,\,$ $(x-a)^2$ $+$ $(y-r)^2$ $\,=\,$ $r^2$

In this case, $OC \,=\, r \,=\, b$. Therefore, it can also be written as follows.

$\,\,\,\therefore\,\,\,\,\,\,$ $(x-a)^2$ $+$ $(y-b)^2$ $\,=\,$ $b^2$

The above two mathematical equations represent the equation of a circle when the circle is touching the horizonal $x$-axis at a point.

The circle’s equation can also be expanded as per the square of difference formula.

$\implies$ $x^2$ $+$ $a^2$ $-$ $2ax$ $+$ $y^2$ $+$ $b^2$ $–$ $2by$ $\,=\,$ $b^2$

$\implies$ $x^2$ $+$ $y^2$ $-$ $2ax$ $–$ $2by$ $+$ $a^2$ $+$ $b^2$ $\,=\,$ $b^2$

$\implies$ $x^2$ $+$ $y^2$ $-$ $2ax$ $–$ $2by$ $+$ $a^2$ $+$ $b^2$ $-$ $b^2$ $\,=\,$ $0$

$\implies$ $x^2$ $+$ $y^2$ $-$ $2ax$ $–$ $2by$ $+$ $a^2$ $+$ $\cancel{b^2}$ $-$ $\cancel{b^2}$ $\,=\,$ $0$

$\,\,\,\therefore\,\,\,\,\,\,$ $x^2$ $+$ $y^2$ $-$ $2ax$ $–$ $2by$ $+$ $a^2$ $\,=\,$ $0$

It is the equation of a circle when the circle is touching the $x$-axis at a point. It can also be expressed as follows by substituting $b$ by $r$.

$\,\,\,\therefore\,\,\,\,\,\,$ $x^2$ $+$ $y^2$ $-$ $2ax$ $–$ $2ry$ $+$ $a^2$ $\,=\,$ $0$

Alternative form

If you take $C (h, k)$, then the equation of a circle when the circle touches the $x$-axis are written as follows.

Simple form

$(x-h)^2+(y-k)^2 \,=\, k^2$

Expansion

$x^2$ $+$ $y^2$ $-$ $2hx$ $–$ $2ky$ $+$ $h^2$ $\,=\,$ $0$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.