Center or Centre of a circle

An internal point that maintains equal distance from every point on a circle is called the center (or centre) of a circle.

Introduction

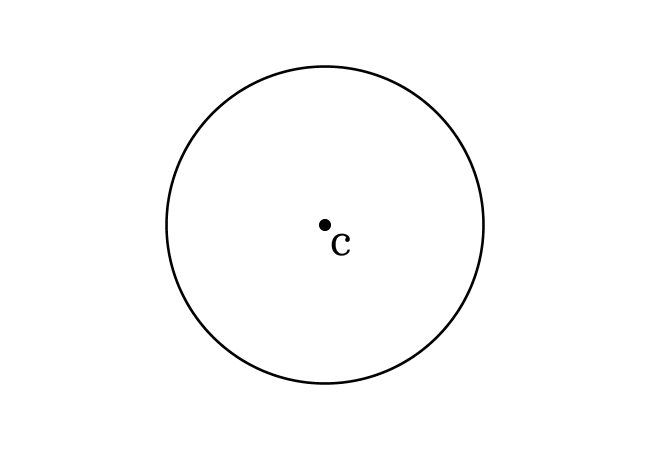
There are numerous points inside every circle and each point has different distances from every point on the circle.

However, there is only one point, which maintains same distance from every point on the circle and that internal point is called the center of a circle.

Now, it is your time learn the fundamental concept of centre (or center) of a circle from an understandable graphical example.

Example

Let $A, B, C$ and $D$ be four points inside a circle and they are located at four different positions in the plane.

1. The Point $A$ is very close to the circle at left-top side. So, it cannot maintain equal distance from all the points on the circle.
2. The Point $B$ is near to the right side of the circle. So, it does not maintain equal distance from all the points on the circle.
3. The Point $C$ is exactly middle to the circle in all the directions. So, it can maintain equal distance from every point on the circle.
4. The Point $D$ is close to the circle at left-bottom side. So, it can’t maintain equal distance from all the point on the the circle.

The locations of points $A$, $B$ and $D$ do not allow them to maintain equal distance from all the points on the circle but the location of point $C$ is exactly middle to the circle in all the directions. Hence, the point $C$ is called the center (or centre) of the circle.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.