Abscissa

The horizontal distance of a point from origin in two dimensional space is called the abscissa. It is also called as the $x$-coordinate.

Introduction

The abscissa is a geometric coordinate of a point, which is useful to know how far the point is from origin in horizontal direction in two dimensional Cartesian coordinate system.

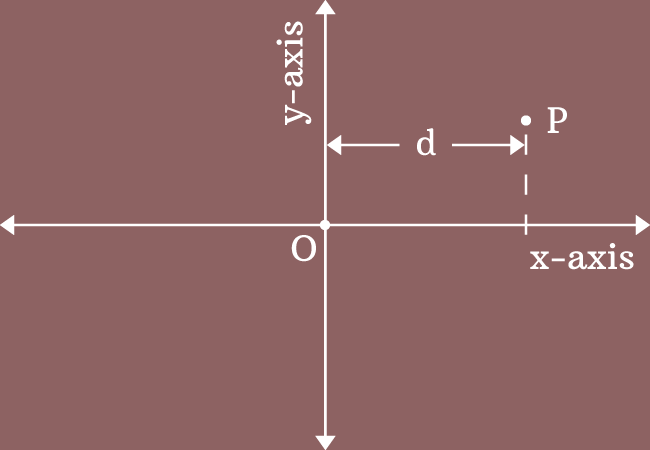
It is measured from origin in horizontal direction by comparing the number line on the $x$-axis. Hence, the abscissa is also called as the $x$-coordinate of the point.

While measuring the abscissa or $x$-coordinate of a point, the $y$-axis is considered as base line because the $y$-axis is passed through the origin in bi-dimensional Cartesian coordinate system.

Here, $P$ is a point on the plane and the horizontal distance of this point is measured as $d$ units from origin by comparing it with the number line on $x$-axis and also taking $y$-axis as base line.

The horizontal distance $d$ is called the abscissa or $x$-coordinate of the point $P$.

Steps

There are two simple steps to find the abscissa of any point in geometry.

1. From any point, draw a perpendicular line to $x$-axis.
2. The distance from origin to the intersecting point of the perpendicular line on $x$-axis is the abscissa or $x$-coordinate.

Example

Let’s learn how to measure the abscissa or $x$-coordinate of any point from an understandable example.

Let $A$, $B$, $C$ and $D$ be four points in a Bi-dimensional Cartesian coordinate system. Now, use the above two steps to determine the $x$-coordinate of each point.

1. The abscissa of point $A$ is $4$.
2. The $x$-coordinate of point $B$ is $-3$
3. The abscissa of point $C$ is $-2$.
4. The $x$-coordinate of point $D$ is $1$

Remember, the number line on the $x$-axis is considered while measuring the $x$-coordinate. So, no need to look at the number line on the $y$-axis.

Thus, the abscissa or $x$-coordinate of any point can be determined geometrically.

Copyright © 2012 - 2022 Math Doubts, All Rights Reserved